
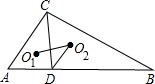
 如图,△ABC中,CD⊥AB于D,O1、O2分别为△ACD和△BCD的内心,若AD=6,CD=8,BD=15,则cos∠O1O2D的值为$\frac{3\sqrt{13}}{13}$.
如图,△ABC中,CD⊥AB于D,O1、O2分别为△ACD和△BCD的内心,若AD=6,CD=8,BD=15,则cos∠O1O2D的值为$\frac{3\sqrt{13}}{13}$. 分析 由O1、O2分别为△ACD和△BCD的内心,得到角平行线,证得∠O1DO2=90°,过O1、O2分别作MO1⊥AB于M,NO2⊥AB与M,得到等腰直角三角形,求得O1D,O2D,再由勾股定理求出O1O2,利用三角函数得到结果.
解答  解:连接O1D,
解:连接O1D,
∵O1、O2分别为△ACD和△BCD的内心,
∴∠CDO1=∠CDO2=45°,
过O1、O2分别作O1M⊥AB于M,NO2⊥AB与N,
∵CD⊥AB,
∴AC=$\sqrt{{AD}^{2}{+CD}^{2}}$=10,BC=$\sqrt{{BD}^{2}{+CD}^{2}}$=17,
∴O1M=$\frac{AD+CD-AC}{2}$=2,O2N=$\frac{CD+BD-BC}{2}$=3,
∴O1D=2$\sqrt{2}$,DO2=3$\sqrt{2}$,
∴O1O2=$\sqrt{{(2\sqrt{2})}^{2}{+(3\sqrt{2})}^{2}}$=$\sqrt{26}$,
∴cos∠O1O2D=$\frac{3\sqrt{2}}{\sqrt{26}}$=$\frac{3\sqrt{13}}{13}$.
故答案为:$\frac{3\sqrt{13}}{13}$.
点评 本题考查了三角形的内切圆,角平分线的性质,等腰直角三角形的性质,勾股定理的应用,正确的作出辅助线是解决本题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:填空题
 燃灯佛舍利塔(简称燃灯塔)是通州八景之一,该塔始建于南北朝北周宇文时期,距今已有1300多年历史.燃灯塔距运河300米,是通州的象征.某同学想利用相似三角形的有关知识来求燃灯塔的高度.他先测量出燃灯塔落在地面上的影长为12米,然后在同一时刻立一根高2米的标杆,测得标杆影长为0.5米,那么燃灯塔高度为48m米.
燃灯佛舍利塔(简称燃灯塔)是通州八景之一,该塔始建于南北朝北周宇文时期,距今已有1300多年历史.燃灯塔距运河300米,是通州的象征.某同学想利用相似三角形的有关知识来求燃灯塔的高度.他先测量出燃灯塔落在地面上的影长为12米,然后在同一时刻立一根高2米的标杆,测得标杆影长为0.5米,那么燃灯塔高度为48m米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 中国象棋中历来有“马”走“日”,“象”飞“田”之说,其意思是:在象棋棋盘上,“马”的走法如下:以“马”所在的位置为棋格所组成的任一“日”字的一个顶点,下一步“马”可以走到该“日”字与原位置相对的那个顶点,如图1马可以自A走到C(或自C走到A)也可自B走到D(或D走到B),在如图棋盘中,建立如图2所示直角坐标系:
中国象棋中历来有“马”走“日”,“象”飞“田”之说,其意思是:在象棋棋盘上,“马”的走法如下:以“马”所在的位置为棋格所组成的任一“日”字的一个顶点,下一步“马”可以走到该“日”字与原位置相对的那个顶点,如图1马可以自A走到C(或自C走到A)也可自B走到D(或D走到B),在如图棋盘中,建立如图2所示直角坐标系:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}$$\sqrt{3}$cm,则EF的长为$\sqrt{3}$cm.
如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}$$\sqrt{3}$cm,则EF的长为$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向左平移2个单位,再向下平移2个单位 | |
| B. | 向右平移2个单位,再向上平移2个单位 | |
| C. | 向左平移1个单位,再向上平移1个单位 | |
| D. | 向右平移1个单位,再向下平移1个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com