
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ᣬ
�ᣬ ![]() ��ֱ��ڵ�A��B��������
��ֱ��ڵ�A��B��������![]() ������A�͵�B����x�����һ������ΪC������D�ӵ�A��������ÿ��1����λ���ȵ��ٶ���O���˶���ͬʱ����E�ӵ�B��������ÿ��2����λ���ȵ��ٶ���A���˶������˶���ʱ��Ϊt�룬0��t��5.
������A�͵�B����x�����һ������ΪC������D�ӵ�A��������ÿ��1����λ���ȵ��ٶ���O���˶���ͬʱ����E�ӵ�B��������ÿ��2����λ���ȵ��ٶ���A���˶������˶���ʱ��Ϊt�룬0��t��5.
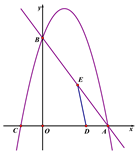
��1���������ߵĽ���ʽ��
��2����tΪ��ֵʱ����A��D��EΪ��������������AOB���ƣ�
��3������ADEΪ����������ʱ����t��ֵ��
��4�����������Ƿ����һ��F��ʹ����A��B��D��FΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д��F������ꣻ�������ڣ�˵������.
���𰸡���1�������ߵĽ���ʽΪ![]() ��
��
��2��t��ֵΪ![]() ��
��![]() ��
��
��3��t��ֵΪ![]() ��
��![]() ��
��![]() ��
��
��4�����������ĵ�F���ڣ���������![]() ��4��8����
��4��8����![]() ��-8��.
��-8��.
����������1����B��C��������꣬���ô���ϵ��������������ߵĽ���ʽ����2�����á�ADE�ס�AOB�͡�AED�ס�AOB�������t��ֵ����3����E��EH��x���ڵ�H����D��DM��AB�ڵ�M�������t��ֵ����4���ֵ�ADΪ��ʱ����ADΪ�Խ���ʱ���������ĵ�F������.
�⣺(1)A��6,0����B��0,8����������֪![]() �����
����� ��
��
��![]() .
.
(2)�� A��6,0����B��0,8������OA=6��OB=8��AB=10����AD=t��AE=10-2t��
�ٵ���ADE�ס�AOBʱ�� ![]() ����
����![]() ����
����![]() ��
��
�ڵ���AED�ס�AOBʱ�� ![]() ����
����![]() ����
����![]() ��
��
����������t��ֵΪ![]() ��
��![]() .
.
(3) �ٵ�AD=AEʱ��t=10-2t����![]() ��
��
�ڵ�AE=DEʱ����E��EH��x���ڵ�H����AD=2AH���ɡ�AEH�ס�ABO�ã�AH=![]() ����
����![]() ����
����![]() ��
��
�۵�AD=DEʱ����D��DM��AB�ڵ�M����AE=2AM���ɡ�AMD�ס�AOB�ã�AM=![]() ����
����![]() ����
����![]() ��
��
����������t��ֵΪ![]() ��
��![]() ��
��![]() .
.
(4) �ٵ�ADΪ��ʱ����BF��x�ᣬ��![]() �����x=4����F��4��8����
�����x=4����F��4��8����
�ڵ�ADΪ�Խ���ʱ����![]() ����
����![]() �����
�����![]() ����x��0����
����x��0����![]() ����
����![]() .
.
�������������������ĵ�F���ڣ���������![]() ��4��8����
��4��8����![]() ��-8��.
��-8��.
���㾦�����⿼����κ����ۺ��⡢���������ε�֪ʶ������Ĺؼ���ѧ�����ϵ����ȷ����������ʽ��ѧ��������ۣ��÷��̵�˼�������⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1��Լ��������Ϊһ���µ�������ţ��ȹ۲����и�ʽ��
1��3=1��4+3=7��3������1��=3��4��1=11��5�� ![]() =5��4+
=5��4+ ![]() =
= ![]() ��
��
5��4=5��4+4=24��4������3��=4��4��3=13������ ![]() ����0=����
����0=���� ![]() ����4+0=��
����4+0=�� ![]()
��
�������ϵ��������д��a��b= ��
��2�����ݣ�1����Լ����a��b����������������ٺ͢�
������x��3����x��ֵ����13����x��ֵ��
����2m��n=2������㣺��m��n������2m+n����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ��,���������о���![]() ������������,�õ��������������ε������ı���ʽΪ12+22+32+��+n2.��nΪ100ʱ,Ӧ��μ��������εľ��������?�������Ǿ�һ����̽��������������.����,ͨ��̽�������Ѿ�֪��:
������������,�õ��������������ε������ı���ʽΪ12+22+32+��+n2.��nΪ100ʱ,Ӧ��μ��������εľ��������?�������Ǿ�һ����̽��������������.����,ͨ��̽�������Ѿ�֪��: ![]() ��
��![]() ʱ,���ǿ���������:
ʱ,���ǿ���������:
(1)�۲첢����:
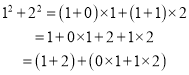 ;
;
![]()
=![]()
=![]() ;
;
![]()
=![]()
=![]() ( );��
( );��
(2)���ɽ��ۣ�
![]() ��
��![]() ��
��![]()
=![]() ��
��![]()
=( )+[ ]
= +
=![]() .
.
(3)ʵ��Ӧ��:
ͨ������̽������,���ǾͿ��������nΪ100ʱ,�����������������ε��ܸ����� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ��� ![]() �У�
�� ![]() ��
�� ![]() ����
���� ![]() ��
�� ![]() ����һ�㣬����
����һ�㣬���� ![]() ��
�� ![]() ��������
�������� ![]() �ڵ�
�ڵ� ![]() ��������
�������� ![]() �ڵ�
�ڵ� ![]() ��
��
��1����ͼ1���� ![]() ����
���� ![]() �ȣ�
�ȣ�
��2������ ![]() ��
�� ![]() ��
�� ![]() Ϊ������������ǵȱ�������ʱ����������ͼ2�в�ȫͼ�β���
Ϊ������������ǵȱ�������ʱ����������ͼ2�в�ȫͼ�β��� ![]() �ij���
�ij���
��3������ ![]() ��
�� ![]() ��
�� ![]() ������
������ ![]() �ڵ�
�ڵ� ![]() ����̽������
����̽������ ![]() Ϊ��ֵʱ����
Ϊ��ֵʱ���� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() Ϊ������ı�����ƽ���ı��Σ�
Ϊ������ı�����ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��F��B��C�ǰ�ԲO�ϵ��ĸ��㣬�ı���OABC��ƽ���ı��Σ���FAB��15�㣬����OF��AB�ڵ�E������C��CD��OF��AB���ӳ����ڵ�D���ӳ�AF��ֱ��CD�ڵ�H.
��1����֤��CD�ǰ�ԲO�����ߣ�
��2����DH��![]() ����EF�ij��Ͱ뾶OA�ij�.
����EF�ij��Ͱ뾶OA�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
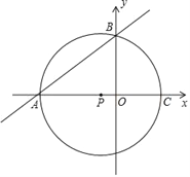
����Ŀ����ͼ����A������Ϊ����8��0������P������Ϊ��-![]() ��0����ֱ��y=
��0����ֱ��y=![]() x+b����A����y���ڵ�B���Ե�PΪԲ�ģ���PAΪ�뾶��Բ��x���ڵ�C��
x+b����A����y���ڵ�B���Ե�PΪԲ�ģ���PAΪ�뾶��Բ��x���ڵ�C��
��1���жϵ�B�Ƿ��ڡ�P�ϣ�˵�����ɣ�
��2�����A��B��C����������ߵĽ���ʽ���������������P����һ������ΪD�����꣮
��3����P���Ƿ����һ��Q��ʹ��A��P��B��QΪ������ı��������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1����ͼ�٣���AOB=60�㣬ODƽ�֡�BOC��OEƽ�֡�AOC�����EOD=�ȣ�
��2������AOB=90�㣬�����������䣬���EOD=;
��3������AOB=���������������䣬���EOD= ��
��4�����Ӧ�ã���ͼ�ڣ���֪�߶�AB��C���߶�AB����һ�㣬D��E�ֱ���AC��CB���е㣬�Բ���DE��AB��������ϵΪ �� ��д�������̣�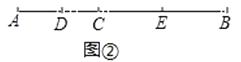
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ǡ�ABC�����߳����ҷ���a��1+x2��+2bx��c��1��x2��=0��������ȣ����ABCΪ��������
A. ���������� B. ֱ�������� C. �ȱ������� D. ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ��ֱ�����ǰ壨�Ƕȷֱ�Ϊ30�㡢60�㡢90���45�㡢45�㡢90�㣩����ͼ(1)��ʾ������һ�����ǰ��ֱ�DZ�AC��ֱ�����ᣬAC���е������ԭ��O��AC��8��б��AB�������ڵ�G����G��Ӧ�����ϵ�����4����һ�����ǰ��ֱ�DZ�AE�������ڵ�F��б��AD�������ڵ�H��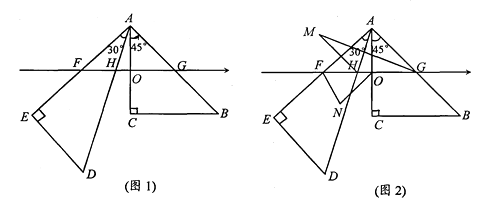
��1�������AGH�������10����AHF�������8�����F��Ӧ�������ϵ����� �� ��H��Ӧ�������ϵ�������
��2����ͼ(2)�����AHF��ƽ���ߺ͡�AGH��ƽ���߽��ڵ�M������HAO��a������a����ʾ��M�Ĵ�С����д���������̣�
��3����ͼ(2)�����AHF��ƽ���ߺ͡�AGH��ƽ���߽��ڵ�M�����EFH��ƽ���ߺ�
��FOC��ƽ���߽��ڵ�N�����N����M��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com