
【题目】如图1,在矩形ABCD中,AB=8,BC=6,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)如图2,当点N落在BD上时,求t的值;
(2)当正方形PQMN的边经过点O时(包括正方形PQMN的顶点),求此时t的值;
(3)当点P在边AD上运动时,求S与t之间的函数关系式;
(4)写出在点P运动过程中,直线DN恰好平分△BCD面积时t的所有可能值.
【答案】
(1)
解:当点N落在BD上时,如图1.
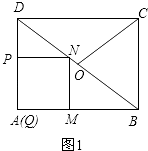
∵四边形PQMN是正方形,
∴PN∥QM,PN=PQ=t.
∴△DPN∽△DQB.
∴ ![]() =
= ![]() ,
,
∵PN=PQ=PA=t,DP=6﹣t,QB=AB=8,
∴ ![]() =
= ![]() ,
,
∴t= ![]() .
.
∴当t= ![]() s时,点N落在BD上
s时,点N落在BD上
(2)
解:①如图2
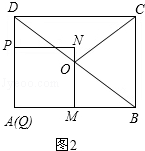 ,
,
则有QM=QP=t,MB=8﹣t.
∵四边形PQMN是正方形,
∴MN∥DQ.
∵点O是DB的中点,
∴QM=BM.
∴t=8﹣t.
∴t=4.
②如图3,
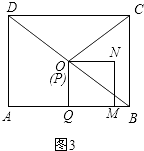
∵四边形ABCD是矩形,
∴∠A=90°.
∵AB=8,AD=6,
∴DB=10.
∵点O是DB的中点,
∴DO=5,
∴1×t=AD+DO=6+5.
∴t=11.
∴当t=4s或11s时,正方形PQMN的边经过点O
(3)
解:①当0<t≤ ![]() 时,如图4.
时,如图4.
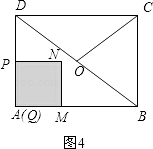
S=S正方形PQMN=PQ2=PA2=t2.
②当 ![]() <t≤6时,如图5,
<t≤6时,如图5,
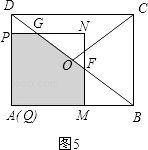
∵tan∠ADB= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
∴PG=8﹣ ![]() t.
t.
∴GN=PN﹣PG=t﹣(8﹣ ![]() t)=
t)= ![]() t﹣8.
t﹣8.
∵tan∠NFG=tan∠ADB= ![]() ,
,
∴ ![]() =
= ![]() .
.
∴NF= ![]() GN=
GN= ![]() (
( ![]() ﹣8)=
﹣8)= ![]() t﹣6.
t﹣6.
∴S=S正方形PQMN﹣S△GNF
=t2﹣ ![]() ×(
×( ![]() t﹣8)×(
t﹣8)×( ![]() t﹣6
t﹣6
=﹣ ![]() t2+14t﹣24.
t2+14t﹣24.
综上所述:当0<t≤ ![]() 时,S=t2.
时,S=t2.
当 ![]() <t≤6时,S=﹣﹣
<t≤6时,S=﹣﹣ ![]() t2+14t﹣24
t2+14t﹣24
(4)
解:设直线DN与BC交于点E,
∵直线DN平分△BCD面积,
∴BE=CE=3.
①点P在AD上,过点E作EH∥PN交AD于点H,如图7,
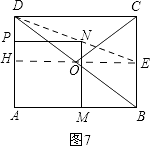
则有△DPN∽△DHE.
∴ ![]() =
= ![]() .
.
∵PN=PA=t,DP=6﹣t,DH=CE=3,EH=AB=8,
∴ ![]() =
= ![]() ,
,
解得;t= ![]() .
.
②点P在DO上,连接OE,如图8,
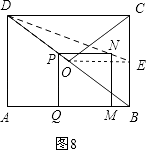
则有OE=4,OE∥DC∥AB∥PN.
∴△DPN∽△DOE.
∴ ![]() =
= ![]() ,
,
∵DP=t﹣6,DO=5,OE=4,
∴PN= ![]() (t﹣6).
(t﹣6).
∵PQ= ![]() (16﹣t),PN=PQ,
(16﹣t),PN=PQ,
∴ ![]() (t﹣6)=
(t﹣6)= ![]() (16﹣t).
(16﹣t).
解得:t= ![]() .
.
综上所述:当直线DN平分△BCD面积时,t的值为 ![]() s或
s或 ![]() s
s
【解析】(1)可证△DPN∽△DQB,从而有 ![]() =
= ![]() ,即可求出t的值.(2)只需考虑两个临界位置(①MN经过点O,②点P与点O重合)下t的值,即可解决问题.(3)根据正方形PQMN与△ABD重叠部分图形形状不同分成二类,如图4、图5,然后运用三角形相似、锐角三角函数等知识就可求出S与t之间的函数关系式.(4)由于点P在折线AD﹣DO运动,可分点P在AD上,点P在DO上两种情况进行讨论,然后运用三角形相似等知识就可求出直线DN平分△BCD面积时t的值.
,即可求出t的值.(2)只需考虑两个临界位置(①MN经过点O,②点P与点O重合)下t的值,即可解决问题.(3)根据正方形PQMN与△ABD重叠部分图形形状不同分成二类,如图4、图5,然后运用三角形相似、锐角三角函数等知识就可求出S与t之间的函数关系式.(4)由于点P在折线AD﹣DO运动,可分点P在AD上,点P在DO上两种情况进行讨论,然后运用三角形相似等知识就可求出直线DN平分△BCD面积时t的值.
【考点精析】根据题目的已知条件,利用相似三角形的性质的相关知识可以得到问题的答案,需要掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.


科目:初中数学 来源: 题型:
【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示.
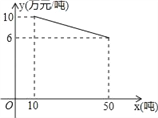
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当生产这种产品每吨的成本为7万元时,求该产品的生产数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F. 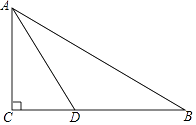
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD= ![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校组织八年级学生进行篮球比赛,八年级(1)班的班长张欢负责买矿泉水给队员喝。张欢到商店去购买A牌矿泉水,该商店对A牌矿泉水的销售方法是:“购买不超过30瓶按零售价销售,每瓶1.5元;多于30瓶但不超过50瓶,按零售价的8折销售;购买多于50瓶,按零售价的6折销售.”该班两次共购A牌矿泉水70瓶(第一次多于第二次),共付出90.6元.
(1)该班分两次购买矿泉水比一次性购买70瓶多花了多少钱?
(2)该班第一次与第二次分别购买矿泉水多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达到每毫升6微克,接着就逐步衰减,10小时后血液中含药量为每毫升3微克,每毫升血液中含药量![]() (微克)随时间
(微克)随时间![]() (小时)的变化如图所示,那么成年人规定剂量服药后:
(小时)的变化如图所示,那么成年人规定剂量服药后:
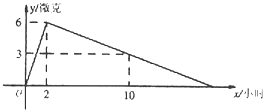
(1)y与x之间的函数关系式.
(2)如果每毫升血液中含药量在4微克或4微克以上时,治疗疾病才是有效的,那么这个有效时
间是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A(﹣1,2),B(2,﹣3)在直线y=kx+b上,则函数y= ![]() 的图象在( )
的图象在( )
A.第一、三象限
B.第一、二象限
C.第二、四象限
D.第二、三象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,三角形ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(2,4),点B的坐标为(1,1),点C的坐标为(3,2).
(1)将三角形ABC先沿着x轴负方向平移6个单位,再沿y轴负方向平移2个单位得到三角形A1B1C1,在图中画出三角形A1B1C1;
(2)分别写出A1,B1、C1的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com