
如图所示,现有一张边长为6的正方形纸片 ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP.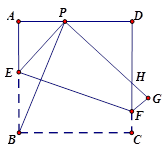
(1)求证:∠APB=∠BPH;
(2)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
(1)通过证明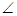 PBC=
PBC=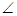 BPH,
BPH,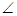 APB=
APB=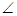 PBC来得出∠APB=∠BPH;(2)存在,当x=3时,S有最小值13.5
PBC来得出∠APB=∠BPH;(2)存在,当x=3时,S有最小值13.5
解析试题分析:解:(1)∵PE=BE,
∴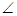 EBP=
EBP=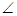 EPB.
EPB.
又∵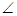 EPH=
EPH=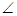 EBC=90°,
EBC=90°,
∴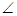 EPH-
EPH-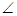 EPB=
EPB=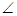 EBC-
EBC-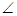 EBP.
EBP.
即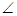 PBC=
PBC=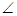 BPH.
BPH.
又∵AD∥BC,
∴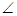 APB=
APB=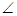 PBC.
PBC.
∴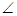 APB=
APB=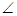 BPH.
BPH.
(2)过F作FM⊥AB,垂足为M,则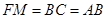 .
.
又EF为折痕,∴EF⊥BP.
∴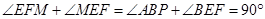 ,
,
∴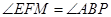 .
.
又∵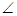 A=
A=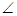 EMF=90°,
EMF=90°,
∴△EFM≌△BPA.
∴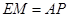 =x.
=x.
∴在Rt△APE中,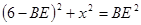 .
.
解得,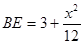 .
.
∴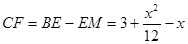 .
.
又四边形PEFG与四边形BEFC全等,
∴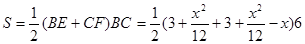 .
.
即: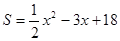 .
.
配方得,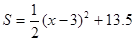 ,∴当x=3时,S有最小值13.5.
,∴当x=3时,S有最小值13.5.
考点:四边形与二次函数
点评:本题主要考查四边形,是一道几何题,把几何题与二次函数相结合,解决本题的关键是找出边、角的关系,列出关系式来,以及就是有关二次函数最值的问题,用配方法求最值


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省徐州市九年级中考模拟数学试卷(解析版) 题型:解答题
如图所示,现有一张边长为6的正方形纸片 ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP.

(1)求证:∠APB=∠BPH;
(2)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(山东德州卷)数学(解析版) 题型:解答题
如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2013年江苏省徐州市中考数学模拟试卷(二)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com