
【题目】已知:如图①,将![]() 的菱形
的菱形![]() 沿对角线
沿对角线![]() 剪开,将
剪开,将![]() 沿射线
沿射线![]() 方向平移,得到
方向平移,得到![]() 点
点![]() 为边
为边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 、点
、点![]() 重合),将射线
重合),将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
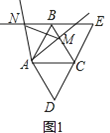
![]() ①求证:
①求证:![]() ;
;
②探究![]() 的形状;
的形状;
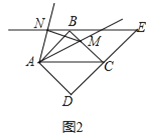
![]() 如图②,若菱形
如图②,若菱形![]() 变为正方形
变为正方形![]() ,将射线
,将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,原题其他条件不变,
,原题其他条件不变,![]() 中的①和②两个结论是否仍然成立?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.
中的①和②两个结论是否仍然成立?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.
【答案】(1)①证明见解析;②△![]() 是等边三角形,理由见解析;(2)①∠
是等边三角形,理由见解析;(2)①∠![]() =∠
=∠![]() 成立,理由见解析;②不成立,△
成立,理由见解析;②不成立,△![]() 是等腰直角三角形,理由见解析.
是等腰直角三角形,理由见解析.
【解析】
(1)①先由菱形可知四边相等,再由∠D=60°得等边△ADC和等边△ABC,则对角线AC与四边都相等,利用ASA证明△ANB≌△AMC,得结论;
②根据有一个角是60°的等腰三角形是等边三角形得出:△AMN是等边三角形;
(2)①成立,根据正方形得45°角和射线AM绕点A逆时针旋转45°,证明△ANB∽△AMC,得∠ANB=∠AMC;
②不成立,△AMN是等腰直角三角形,利用①中的△ANB∽△AMC,得比例式进行变形后,再证明△NAM∽△BAD,则△AMN是等腰直角三角形.
(1)如图1,①∵四边形![]() 是菱形,
是菱形,

∴![]() ,
,
∵∠![]()
![]() 60°,
60°,
∴△ADC和△ABC是等边三角形,
∴![]() ,∠BAC
,∠BAC![]() 60°,
60°,
∵∠![]()
![]() 60°,
60°,
∴∠![]() =∠
=∠![]() ,
,
由△ADC沿射线DC方向平移得到△BCE,可知∠CBE![]() 60°,
60°,
∵∠ABC![]() 60°,
60°,
∴∠ABN![]() 60°,
60°,
∴∠ABN![]() ∠ACB
∠ACB![]() 60°
60°
∴△![]() ≌△
≌△![]() ,
,
∴∠![]() =∠
=∠![]() ;
;
②如图1,△![]() 是等边三角形,理由是:
是等边三角形,理由是:
由△![]() ≌△
≌△![]() ,
,
∴AM![]() AN,
AN,
∵∠![]()
![]() 60°,
60°,
∴△![]() 是等边三角形;
是等边三角形;
(2)①如图2,∠![]() =∠
=∠![]() 成立,理由是:
成立,理由是:

在正方形ABCD中,
∴∠BAC![]() ∠DAC=∠BCA
∠DAC=∠BCA![]() 45°,
45°,
∵∠NAM![]() 45°,
45°,
∴∠![]() =∠
=∠![]() ,
,
由平移得:∠EBC![]() ∠CAD
∠CAD![]() 45°,
45°,
∵∠ABC=90°,
∴∠ABN![]() 180°
180°![]() 90°45°
90°45°![]() 45°,
45°,
∴∠ABN![]() ∠ACM
∠ACM![]() 45°,
45°,
∴△![]() ∽△
∽△![]() ,
,
∴∠![]() =∠
=∠![]() ;
;
②如图2,不成立,
△![]() 是等腰直角三角形,理由是:
是等腰直角三角形,理由是:
∵△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠![]() =∠
=∠![]() =45°,
=45°,
∴△![]() ∽△
∽△![]() ,
,
∴∠![]() =∠
=∠![]() =90°,
=90°,
∴△![]() 是等腰直角三角形.
是等腰直角三角形.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐 标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
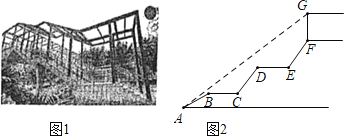
【题目】为了方便学生在上下学期间安全过马路,南岸区政府决定在南开(融侨)中学校门口修建人行天桥(如图1),其平面图如图2所示,初三(8)班的学生小刘想利用所学知识测量天桥顶棚距地面的高度.天桥入口A点有一台阶AB=2m,其坡角为30°,在AB上方有两段平层BC=DE=1.5m,且BC,DE与地面平行,BC,DE上方又紧接台阶CD,EF,其长度相等且坡度均为i=4:3,顶棚距天桥距离FG=2m,且小刘从入口A点测得顶棚顶端G的仰角为37°,请根据以上数据,帮小刘计算出顶端G点距地面高度为( )m.(结果保留一位小数,参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
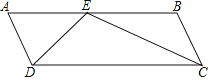
【题目】如图,在平行四边形ABCD中,∠B=120°,AB与CD之间的距离是![]() ,AB=28,在AB上取一点E(AE<BE),使得∠DEC=120°,则AE=_____.
,AB=28,在AB上取一点E(AE<BE),使得∠DEC=120°,则AE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
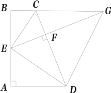
【题目】如图,已知四边形ABCD中,AB⊥AD,BC∥AD,E为AB的中点,且EC、ED分别为∠BCD、∠ADC的角平分线,EF⊥CD交BC的延长线于点G,连接DG.
(1)求证:CE⊥DE;
(2)若AB=6,求CF·DF的值;
(3)当△BCE与△DFG相似时,![]() 的值是 .
的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
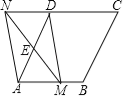
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4张相同的卡片上分别写有数字1、2、3、4,将卡片背面朝上,洗匀后从中任意抽取1张,将卡片上的数字作为被减数;一只不透明的袋子中装有标号为1、2、3的3个小球,这些球除标号外都相同,搅匀后从中任意摸出1个球,将摸到的球的标号作为减数.
(1)求这两个数的差为0的概率;
(2)游戏规则规定:当抽到的这两个数的差为非负数时,甲获胜;否则,乙获胜.这样的规则公平吗?如果不公平,请设计一个公平的规则,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
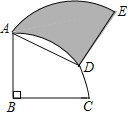
【题目】如图,将半径为4,圆心角为90°的扇形BAC绕A点逆时针旋转60°,点B、C的对应点分别为点D、E且点D刚好在![]() 上,则阴影部分的面积为_____.
上,则阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
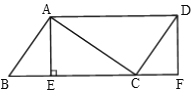
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,点F在BC延长线上,且CF=BE,连接AC,DF,
(1)求证:四边形AEFD是矩形;
(2)若∠ACD=90°,CF=3,DF=4,求AD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com