
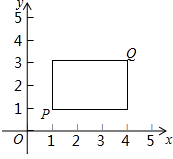
 在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.
在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.分析 (1)①由相关矩形的定义可知:要求A与B的相关矩形面积,则AB必为对角线,利用A、B两点的坐标即可求出该矩形的底与高的长度,进而可求出该矩形的面积;
②由定义可知,AC必为正方形的对角线,所以AC与x轴的夹角必为45,设直线AC的解析式为;y=kx+b,由此可知k=±1,再(1,0)代入y=kx+b,即可求出b的值;
(2)由定义可知,MN必为相关矩形的对角线,若该相关矩形的为正方形,即直线MN与x轴的夹角为45°,由因为点N在圆O上,所以该直线MN与圆O一定要有交点,由此可以求出m的范围.
解答 解:(1)①∵A(1,0),B(3,1)
由定义可知:点A,B的“相关矩形”的底与高分别为2和1,
∴点A,B的“相关矩形”的面积为2×1=2;
②由定义可知:AC是点A,C的“相关矩形”的对角线,
又∵点A,C的“相关矩形”为正方形
∴直线AC与x轴的夹角为45°,
设直线AC的解析为:y=x+m或y=-x+n
把(1,0)分别y=x+m,
∴m=-1,
∴直线AC的解析为:y=x-1,
把(1,0)代入y=-x+n,
∴n=1,
∴y=-x+1,
综上所述,若点A,C的“相关矩形”为正方形,直线AC的表达式为y=x-1或y=-x+1;
(2)设直线MN的解析式为y=kx+b,
∵点M,N的“相关矩形”为正方形,
∴由定义可知:直线MN与x轴的夹角为45°,
∴k=±1,
∵点N在⊙O上,
∴当直线MN与⊙O有交点时,点M,N的“相关矩形”为正方形,
当k=1时,
作⊙O的切线AD和BC,且与直线MN平行,
其中A、C为⊙O的切点,直线AD与y轴交于点D,直线BC与y轴交于点B,
连接OA,OC,
把M(m,3)代入y=x+b,
∴b=3-m,
∴直线MN的解析式为:y=x+3-m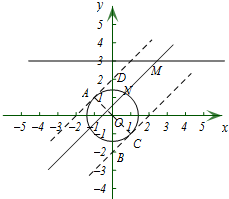
∵∠ADO=45°,∠OAD=90°,
∴OD=$\sqrt{2}$OA=2,
∴D(0,2)
同理可得:B(0,-2),
∴令x=0代入y=x+3-m,
∴y=3-m,
∴-2≤3-m≤2,
∴1≤m≤5,
当k=-1时,把M(m,3)代入y=-x+b,
∴b=3+m,
∴直线MN的解析式为:y=-x+3+m,
同理可得:-2≤3+m≤2,
∴-5≤m≤-1;
综上所述,当点M,N的“相关矩形”为正方形时,m的取值范围是:1≤m≤5或-5≤m≤-1
点评 本题考查新定义问题,涉及圆的切线性质,矩形的性质,正方形的性质,解答本题需要我们理解相关矩形的定义,对学生的综合能力要求较高,一定要注意将新旧知识贯穿起来.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:填空题
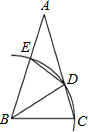 △ABC中,AB=AC,∠A=30°,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连结BD,DE. 则∠BDE的度数为67.5°.
△ABC中,AB=AC,∠A=30°,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连结BD,DE. 则∠BDE的度数为67.5°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
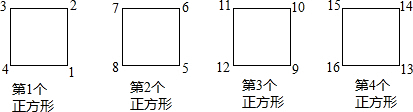
| A. | 第504个正方形的左下角 | B. | 第504个正方形的右下角 | ||
| C. | 第505个正方形的左下角 | D. | 第505个正方形的右下角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知等边△ABC的边长为8,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为( )
如图,已知等边△ABC的边长为8,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为( )| A. | 3 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 为了了解某车间工人日加工零件数的情况,车间负责人通过统计数据绘制成如图所示的条形统计图,则下列说法正确的是( )
为了了解某车间工人日加工零件数的情况,车间负责人通过统计数据绘制成如图所示的条形统计图,则下列说法正确的是( )| A. | 这些工人日加工零件数的众数是10个,中位数是7个 | |
| B. | 这些工人日加工零件数的众数是6个,中位数是6个 | |
| C. | 这些工人日加工零件数的众数是10个,中位数是5.5个 | |
| D. | 这些工人日加工零件数的众数是6个,中位数是5.5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,△ABC与△A1B1C1是以点P为位似中心的位似图形,且顶点都在格点上,则点P的坐标为( )
如图,在平面直角坐标系中,△ABC与△A1B1C1是以点P为位似中心的位似图形,且顶点都在格点上,则点P的坐标为( )| A. | (-4,-3) | B. | (-3,-3) | C. | (-4,-4) | D. | (-3,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com