
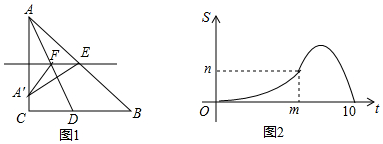
分析 (1)根据图2可知AB=10,由角平分线可得AC和BC的长,根据图1和图2确定重叠部分面积的分界处:当A′E过D时,即为t=m时,如图3,列等式求t的值即可;
(2)①当0≤t≤$\frac{55}{8}$时,如图4,设A′E与AD交于点G,过G作GH⊥PE于H,△A′EF与△ABD重叠部分是△EFG,根据三角形面积公式可得结果;
②当$\frac{55}{8}$<t≤10时,如图5,△A′EF与△ABD重叠部分是梯形FDHE,利用面积差可得结果.
解答 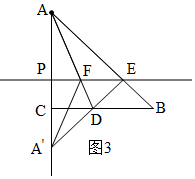 解:(1)如图1,∵点A的对称A′落在射线AC上,
解:(1)如图1,∵点A的对称A′落在射线AC上,
∴EF⊥AC,且EF是AA′的中垂线,
由图2可知:0≤t≤10,
∴AB=10×1=10,
∵AD平分∠BAC,
∴$\frac{AC}{AB}=\frac{CD}{BD}$=$\frac{3}{5}$,
∴AC=6,BC=8,
∴CD=3,
当t=m时,A′E过点D,如图3,
则AE=t,
cos∠CAB=$\frac{AP}{AE}=\frac{AC}{AB}$=$\frac{3}{5}$,
∴$\frac{AP}{t}=\frac{3}{5}$,
∴AP=$\frac{3}{5}t$,
∴PC=AC-AP=6-$\frac{3}{5}t$,
∵EF是AA′的中垂线,
∴AE=A′E,
∴∠AA′E=∠A′AE,
∴tan∠AA′E=tan∠A′AE=$\frac{CD}{A′C}=\frac{BC}{AC}$=$\frac{8}{6}$,
∴$\frac{3}{A′C}=\frac{8}{6}$,
∴A′C=$\frac{9}{4}$,
∵AA′=2AP=AC+A′C,
∴2×$\frac{3}{5}t$=6+$\frac{9}{4}$,
t=$\frac{55}{8}$,
即m=$\frac{55}{8}$,
故答案为:3,$\frac{55}{8}$;
(2)①当0≤t≤$\frac{55}{8}$时,如图4,设A′E与AD交于点G,过G作GH⊥PE于H,
由(1)知:AE=t,PE=$\frac{4}{5}$t,
∵$\frac{PF}{EF}=\frac{3}{5}$,
∴EF=$\frac{5}{8}$PE=$\frac{5}{8}×\frac{4}{5}t$=$\frac{1}{2}t$,
∵AG平分∠A′AE,
∴$\frac{A′G}{GE}=\frac{AA′}{AE}$=$\frac{2×\frac{3}{5}t}{t}$=$\frac{6}{5}$,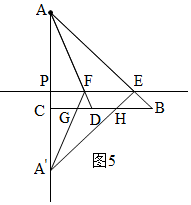
∵GH∥A′P,
∴△GHE∽△A′PE,
∴$\frac{GH}{A′P}=\frac{GE}{A′E}$,
∴$\frac{GH}{\frac{3}{5}t}$=$\frac{5}{11}$,
∴GH=$\frac{3}{11}$t,
∴S=S△GEF=$\frac{1}{2}$EF•GH=$\frac{1}{2}$$•\frac{1}{2}t•\frac{3}{11}t$=$\frac{3}{44}{t}^{2}$;
②当$\frac{55}{8}$<t≤10时,如图5,
∵AP=A′P=$\frac{3}{5}t$,
∴PC=AC-AP=6-$\frac{3}{5}t$,
A′C=AA′-AC=$\frac{6}{5}t$-6,
Rt△A′CH中,tan∠CA′H=$\frac{CH}{A′C}$=$\frac{BC}{AC}=\frac{8}{6}$,
∴CH=$\frac{4}{3}$($\frac{6}{5}t$-6)=$\frac{8}{5}t-8$,
∴BH=BC-CH=8-($\frac{8}{5}t-8$)=16-$\frac{8}{5}t$,
∴S=S四边形FDHE=S梯形FDBE-S△BEH=$\frac{1}{2}$PC•(EF+BD)-$\frac{1}{2}$PC•BH,
=$\frac{1}{2}$PC•(EF+BD-BH),
=$\frac{1}{2}$(6-$\frac{3}{5}$t)($\frac{1}{2}$t+5-16+$\frac{8}{5}$t),
=-$\frac{63}{100}{t}^{2}+\frac{48}{5}t-33$;
综上所述,S与t之间的函数关系式为:S=$\left\{\begin{array}{l}{\frac{3}{44}{t}^{2}(0≤t≤\frac{55}{8})}\\{-\frac{63}{100}{t}^{2}+\frac{48}{5}t-33(\frac{55}{8}<t≤10)}\end{array}\right.$.
点评 本题是动点问题的函数图象,此类题有难度,理解图1和图2是关键,注意重叠部分面积的分界外,考查了三角形相似的性质和判定、中垂线的性质、对称的性质.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.5-8 | B. | 85×10-9 | C. | 0.85×10-7 | D. | 8.5×10-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
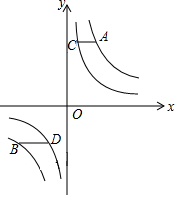 如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )
如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{9}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com