
【题目】如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC , 交AC于D , BC=4 cm.
(1)求证:AC⊥OD;
(2)求OD的长;
【答案】
(1)
证明:∵AB是⊙O的直径,
∴∠C=90°.
∵OD∥BC,
∴∠ADO=∠C=90°.∴AC⊥OD.
(2)
解:∵OD∥BC,
又∵O是AB的中点,
∴OD是△ABC的中位线.
∴OD= ![]() BC=
BC= ![]() ×4=2(cm).
×4=2(cm).
【解析】(1)证明:∵AB是⊙O的直径,
∴∠C=90°.
∵OD∥BC,
∴∠ADO=∠C=90°.∴AC⊥OD.
(2)∵OD∥BC,
又∵O是AB的中点,
∴OD是△ABC的中位线.
∴OD= ![]() BC=
BC= ![]() ×4=2(cm).
×4=2(cm).
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
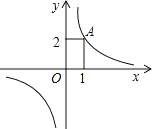
【题目】如上图,反比例函数![]() 的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .
的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .
【答案】(-1,-2)(答案不唯一).
【解析】试题分析:根据“第一象限内的图象经过点A(1,2)”先求出函数解析式,给x一个值负数,求出y值即可得到坐标.
试题解析:∵图象经过点A(1,2),
∴![]()
解得k=2,
∴函数解析式为y=![]() ,
,
当x=-1时,y=![]() =-2,
=-2,
∴P点坐标为(-1,-2)(答案不唯一).
考点:反比例函数图象上点的坐标特征.
【题型】填空题
【结束】
13
【题目】在y轴右侧且平行于y轴的直线l被反比例函数![]() (
(![]() )与函数
)与函数![]() (
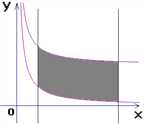
(![]() )所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.
)所截,当直线l向右平移4个单位时,直线l被两函数图象所截得的线段扫过的面积为__________平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的反比例函数,且当x=-4时,y=![]() ,
,
(1)求这个反比例函数关系式和自变量x的取值范围;
(2)求当x=6时函数y的值.
【答案】(1)![]() (2)
(2)![]()
【解析】整体分析:
(1)由反比例函数的这定义求k值,确定x的取值范围;(2)把x=6代入(1)中求得的反比例函数的解析式.
解:(1)设反比例函数关系式为![]() ,
,
则k=-4×![]() =-2,
=-2,
所以个反比例函数关系式是![]() ,自变量x的取值范围是x≠0.
,自变量x的取值范围是x≠0.
(2)当x=6时, ![]() =
=![]() =-
=-![]() .
.
【题型】解答题
【结束】
18
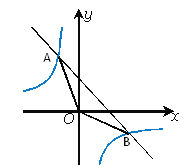
【题目】如图,函数y=![]() 和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
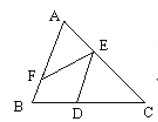
【题目】如图,有下列说法:①若DE∥AB,则∠DEF+∠EFB=180;
②能与∠DEF构成内错角的角的个数有2个;③能与∠BFE构
成同位角的角的个数有2个;④能与∠C构成同旁内角的角的个数有4个.其中结论正确的是( )
A. ①② B. ③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形(长方形),点A、C的坐标分别为A(10,0 ),C(0,4),点D是OA的中点,点P在线段BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 ____________________________________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y=![]() x+3垂直,求解析式.
x+3垂直,求解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com