
【题目】下列关于函数 ![]() 的四个命题:①当
的四个命题:①当 ![]() 时,
时, ![]() 有最小值10;②
有最小值10;② ![]() 为任意实数,
为任意实数, ![]() 时的函数值大于
时的函数值大于 ![]() 时的函数值;③若
时的函数值;③若 ![]() ,且
,且 ![]() 是整数,当
是整数,当 ![]() 时,
时, ![]() 的整数值有
的整数值有 ![]() 个;④若函数图象过点
个;④若函数图象过点 ![]() 和
和 ![]() ,其中
,其中 ![]() ,
, ![]() ,则
,则 ![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A.①
B.②
C.③
D.④
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法——更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也,以等数约之.”意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.例如:求91与56的最大公约数:
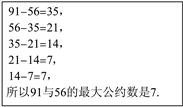
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(n,-2),B(1,4)是一次函数 y=kx+b的图象和反比例函数 ![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
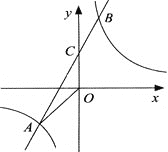
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)观察图象,直接写出反比例函数值大于一次函数值x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数![]() 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则![]() 的值是( )
的值是( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副含 ![]() 和
和 ![]() 角的三角板
角的三角板 ![]() 和
和 ![]() 叠合在一起,边
叠合在一起,边 ![]() 与
与 ![]() 重合,
重合, ![]() (如图1),点
(如图1),点 ![]() 为边
为边 ![]()
![]() 的中点,边
的中点,边 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,此时线段
,此时线段 ![]() 的长是 . 现将三角板
的长是 . 现将三角板 ![]() 绕点
绕点 ![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 ![]() 从
从 ![]() 到
到 ![]() 的变化过程中,点
的变化过程中,点 ![]() 相应移动的路径长共为 . (结果保留根号)
相应移动的路径长共为 . (结果保留根号)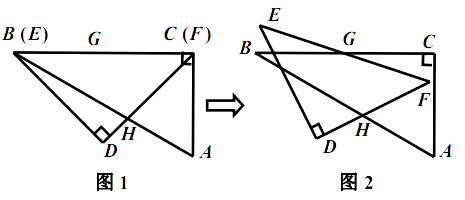
查看答案和解析>>
科目:初中数学 来源: 题型:
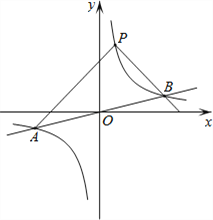
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,点
,点![]() 的横坐标是
的横坐标是
4,点![]() 在反比例函数
在反比例函数![]() 的图像上.
的图像上.
(1)求反比例函数的表达式;
(2)观察图像回答:当![]() 为何值时,
为何值时, ![]() ;
;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
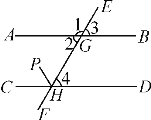
【题目】如图,直线AB,CD被EF所截,点G,H为它们的交点,∠1∶∠2=5∶3,∠2与它的内错角相等,HP平分∠CHG.求:
(1)∠4的度数;
(2)∠CHP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外学习小组在设计一个长方形时钟钟面时,欲使长方形的宽为20厘米,时钟的中心在长方形对角线的交点上,数字2在长方形的顶点上,数字3、6、9、12标在所在边的中点上,如图所示。
(1)问长方形的长应为多少?
(2)请你在长方框上点出数字1的位置,并说明确定该位置的方法;
(3)请你在长方框上点出钟面上其余数字的位置,并写出相应的数字(说明:要画出必要的、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com