
 有理数a、b在数轴上的对应点位置如图所示
有理数a、b在数轴上的对应点位置如图所示科目:初中数学 来源: 题型:解答题
| 入住的房间数量 | 房间价格 | 总维护费用 | |
| 提价前 | 60 | 200 | 60×20 |
| 提价后 | 60-$\frac{x}{10}$ | 200+x | (60-$\frac{x}{10}$)×20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
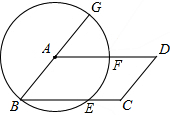 如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧$\widehat{EF}$和弧$\widehat{FG}$是否相等,并说明理由.
如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧$\widehat{EF}$和弧$\widehat{FG}$是否相等,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点O在AC的垂直平分线上 | B. | △AOB、△BOC、△COA都是等腰三角形 | ||
| C. | ∠OAB+∠OBC+∠OCA=90° | D. | 点O到AB、BC、CA的距离相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ABC和∠ACB的角平分线相交于点O,DE经过O点,且DE∥BC.
如图,△ABC中,∠ABC和∠ACB的角平分线相交于点O,DE经过O点,且DE∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x-1)2-3 | B. | y=2(x-1)2+3 | C. | y=2(x+1)2-3 | D. | y=2(x+2)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
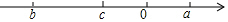 已知a,b,c在数轴上的位置如图所示,且|a|=|c|.
已知a,b,c在数轴上的位置如图所示,且|a|=|c|.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com