
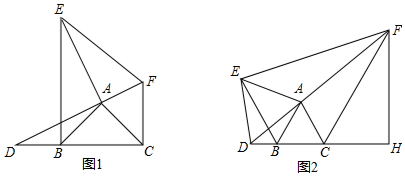
分析 (1)结论:AE=AD,且AE⊥AD.只要证明△EAB≌△DAC即可解决问题.
(2)如图2中,作FM⊥CA交CA的延长线于M,交BE于N.设CH=x,DB=y,AB=BC=AC=a.想办法构建方程组即可解决问题.
解答 解:(1)结论:AE=AD,且AE⊥AD.
理由:如图1中,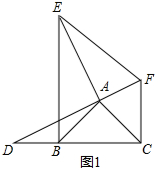
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠EBA=∠ABC=45°,
∴∠EBA=∠ACD,
在△EAB和△DAC中,
$\left\{\begin{array}{l}{EB=CD}\\{∠EBA=∠ACD}\\{BA=CA}\end{array}\right.$,
∴△EAB≌△DAC,
∴AE=AD,∠EAB=∠DAC,
∴∠EAD=∠BAC=90°,
∴AE=AD,且AE⊥AD.
(2)如图2中,作FM⊥CA交CA的延长线于M,交BE于N.设CH=x,DB=y,AB=BC=AC=a.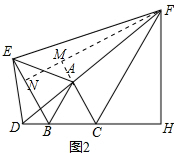
∵BE=CD,BH-BE=2,
∴CH-DB=2,即x-y=2,
∵∠ABD=∠FCD=120°,
∴AB∥CF,
∴$\frac{AB}{CF}$=$\frac{DB}{DC}$,
∴$\frac{a}{2x}$=$\frac{x-2}{x-2+a}$,
∴ax-2a+a2=2x2-4x ①,
在Rt△EFN中,∵EF2=EN2+FN2,
易知FN=$\frac{3}{2}$a-2,MN=$\frac{\sqrt{3}}{2}$a,FM=$\sqrt{3}$x,
∴49=($\frac{3}{2}$a-2)2+($\frac{\sqrt{3}}{2}$a+$\sqrt{3}$x)2,
整理得3(ax-2a+a2)+4+3x2=49 ②,
①代入②得到,6x2-12x+4+3x2=49,
整理得3x2-4x-15=0,
解得x=3或-$\frac{5}{3}$(舍弃),
∴CH=3.
点评 本题考查三角形综合题、等腰直角三角形的性质、等边三角形的性质、全等三角形的判定和性质、平行线分线段成比例定理、勾股定理、二元二次方程组等知识,解题的关键是灵活应用所学知识解决问题,学会用构建方程的思想思考问题,属于中考压轴题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
| 路程(千米) | 运费(元/吨.千米) | |||
| 甲仓库 | 乙仓库 | 甲仓库 | 乙仓库 | |
| A地 | 25 | 20 | 1 | 0.8 |
| B地 | 20 | 15 | 1.2 | 1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
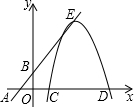 如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.
如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
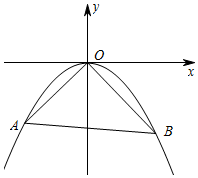 如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)
如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
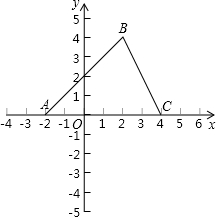 如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).
如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com