练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．下列二次根式，最简二次根式是（　　）
    A．$\sqrt{\frac{1}{5}}$B．$\sqrt{0.5}$C．$\sqrt{5}$D．$\sqrt{50}$

    分析 用判断最简二次根式的条件直接判断．

    解答 解：由判断最简二次根式的条件，得，$\sqrt{5}$是最简二次根式．
    故选C．

    点评 此题是最简二次根式题，熟记最简二次根式的条件是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．如图（1），∠AOB=45°，点P、Q分别是边OA，OB上的两点，且OP=2cm．将∠O沿PQ折叠，点O落在平面内点C处．
    （1）①当PC∥QB时，OQ=2cm；
    ②当PC⊥QB时，求OQ的长．
    （2）当折叠后重叠部分为等腰三角形时，求OQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

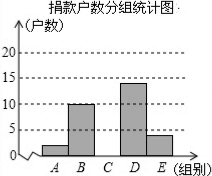    19．为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动，对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）．
                      捐款户数分组统计表
     组别 捐款额（x）元 户数 频率
    A  1≤x＜100 2 0.04
     B 100≤x＜200 10 0.2
     C 200≤x＜300  0.4
     D 300≤x＜400 14 a
     E x≥400 4 0.08
    请结合以上信息解答下列问题．
    （1）a=0.28，本次调查样本的容量是50；
    （2）先求出C组的户数为20户，再补全“捐款户数分组统计图”；
    （3）直接写出捐款额的中位数落在C组．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

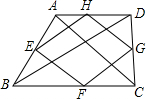    16．如图，顺次连接四边形ABCD各边中点得到四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（　　）
    A．AB∥CDB．AB=CDC．AC⊥BDD．AC=BD

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

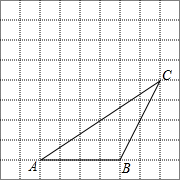    3．如图，△ABC的顶点都在方格纸的格点上，将△ABC向左平移1格，再向上平移3格，其中每个格子的边长为1个长度单位．
    （1）在图中画出平移后的△A′B′C′；
    （2）若连接AA′，CC′，则这两条线段的关系是AA′∥CC′，AA′=CC′；
    （3）作直线l，将△ABC分成两个面积相等的三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．（1）解方程；$\frac{3}{2x-2}$+$\frac{1}{1-x}$=3
    （2）先化简：（$\frac{a+3}{a-2}+\frac{1}{2-a}$）÷$\frac{{a}^{2}-4}{3}$请在2和3中选择一个合适的数代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．解不等式组：$\left\{\begin{array}{l}{2x+1≥-1}\\{\frac{1+2x}{3}＞x-1}\end{array}\right.$，并把不等式组的解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．探究多边形内角和公式时，从n边形的一个顶点出发引出（n-3）条对角线，将n边形分割成（n-2）个三角形，这（n-2）个三角形的所有内角之和即为n边形的内角和，这一探究过程运用的数学思想是（　　）
    A．方程思想B．函数思想C．数形结合思想D．化归思想

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

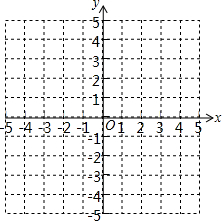    18．△ABC的三个顶点坐标分别为A（2，-1），B（4，-2），C（1，-3），将△ABC平移至△A1B1C1的位置，点A、B、C对应的点分别为A1、B1、C1，已知点A1的坐标是（-2，3）．
    （1）求点B1，C1的坐标；
    （2）在如图的平面直角坐标系中，画出△ABC和△A1B1C1；
    （3）已知△A1B1C1内有一点P1（a，b），直接写出它在△ABC的对应点P的坐标．

    查看答案和解析>>

    同步练习册答案