
分析 基于平均数的考虑:1,2,3,4,…,105的平均数是53,1,2,3,4,…,106的平均数是53.5,它应该有105个或106个连续数,由于减去一个数的平均为53$\frac{3}{7}$,当n=105个,但104×53$\frac{3}{7}$不是整数,故否定了有105个数.当106个数时,可以尝试错误法找出.
解答 解:1,2,3,4,….,105的平均数是53,
1,2,3,4,….,106的平均数是53.5
它应该有105个或106个连续数.
(1)由于减去一个数的平均为53$\frac{3}{7}$,当n=105个,但104×53$\frac{3}{7}$不是整数,故否定了有105个数.
(2)当106个数时,很明显不会删去106,故应是1-105中其中一个数,考虑平均数的分数部,由于是105个数的平均,故将$\frac{3}{7}$=$\frac{45}{105}$,当中表示删去的数为106-45=61,或1+2+3+…+106=5671,
当减去一个数后,平均为53$\frac{3}{7}$,n=105,
和=53$\frac{3}{7}$×105=5610,
所以减去的一个数应是5671-5610=61.
答:删去的那个数是61.
点评 本题考查的是样本平均数的求法及运用,解题的关键是先确定连续自然数介于105个或106个连续数,然后讨论即可.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:填空题
 如图,点P为双曲线y=$\frac{k}{x}$上一点,PE⊥x轴于点E,PF⊥y轴于点F,直线y=-$\frac{1}{2}$x+2与y轴、x轴分别交于点A、B,与PF、PE分别交于点C、D,若AD•BC=10,则k=4.
如图,点P为双曲线y=$\frac{k}{x}$上一点,PE⊥x轴于点E,PF⊥y轴于点F,直线y=-$\frac{1}{2}$x+2与y轴、x轴分别交于点A、B,与PF、PE分别交于点C、D,若AD•BC=10,则k=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
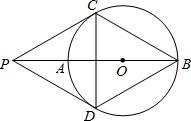 如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )
如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=CD;(4)弧AC=弧AD.其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com