
 x与直线y=kx+b交于点A(m,n)(m>0),点B在直线y=
x与直线y=kx+b交于点A(m,n)(m>0),点B在直线y= x上且与点A关于坐标原点O成中心对称.
x上且与点A关于坐标原点O成中心对称. (1)解1:过点A作AD⊥x轴,垂足为D.
(1)解1:过点A作AD⊥x轴,垂足为D. x上,
x上,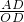 =
= ,
, ,
, ,m=
,m= .
. ,
, ).
). x上
x上 m.
m. ,m=
,m= .
. ,
, ).
). ,0.97).
,0.97).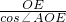
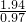
 ,1).
,1). x上,得出∠AOD=30°,进而得出m,n的值,即可得出A点坐标;
x上,得出∠AOD=30°,进而得出m,n的值,即可得出A点坐标;

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 3 |
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源:风华金帆同步训练·数学·七年级下册(新课标人教版) 新课标人教版 题型:013
下列说法中,正确的是
A.有且只有一条直线垂直于已知直线
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
C.互相垂直的两条直线一定相交
D.直线c外一点A与直线c上各点联结而成的所有线段中,最短线段的长是3 cm,则点A到直线c的距离是3 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com