
 水果市场中的甲、乙两家商店中都批发同一种水果,批发水果x千克时,在甲、乙两家商店的批发价分别为y1元和y2元,已知y1和y2关于x的函数图象分别为如图所示的折线OAB和射线OC.
水果市场中的甲、乙两家商店中都批发同一种水果,批发水果x千克时,在甲、乙两家商店的批发价分别为y1元和y2元,已知y1和y2关于x的函数图象分别为如图所示的折线OAB和射线OC.分析 (1)根据射线OC经过点(20,200),即可得到y2与自变量x的函数解析式以及自变量x的取值范围;
(2)由图象可知,当0<x<20时,在乙店批发比较便宜;
(3)过点(30,0)作y轴的平行线,交OC于点E,交AB于点F,即可得到E(30,300),F(30,250),再根据待定系数法进行计算,即可得到射线AB的函数解析式以及自变量x的取值范围.
解答 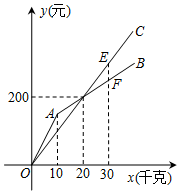 解:(1)∵射线OC经过原点,
解:(1)∵射线OC经过原点,
∴设y2与自变量x的函数关系为y2=k'x(k'≠0),
∵射线OC经过点(20,200),
∴200=20k',
解得k'=10.
∴y2=10x,自变量x的取值范围是x>0.
(2)由图象可知,当0<x<20时,在乙店批发比较便宜.
(3)∵射线OC过点(20,200),射线OC的表达式是y2=10x,
过点(30,0)作y轴的平行线,交OC于点E,交AB于点F.
∴E(30,300),F(30,250),
设射线AB的表达式为y1=kx+b,
∴$\left\{\begin{array}{l}{250=30k+b}\\{200=20k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=5}\\{b=100}\end{array}\right.$.
∴射线AB的表达式为y1=5x+100,自变量x的取值范围是x>10.
点评 本题考查了一次函数的应用、待定系数法等知识,解题的关键是灵活运用一次函数的性质解决问题,学会利用图象解决实际问题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1≥y2 | C. | y1>y2 | D. | y1≤y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届广东省梅州市九年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,等腰直角△ABC中,∠ACB=90°,点E为△ABC内一点,且∠BEC=90°,将△BEC绕C点顺时针旋转90°,使BC与AC重合,得到△AFC,连接EF交AC于点M,已知BC=10,CF=6,则AM:MC的值为( )
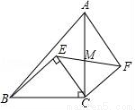
A. 4:3 B. 3:4 C. 5:3 D. 3:5
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
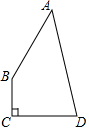 四边形ABCD中,AB=12,BC=3,CD=4,AD=13,且∠C=90°,则四边形ABCD的面积为( )
四边形ABCD中,AB=12,BC=3,CD=4,AD=13,且∠C=90°,则四边形ABCD的面积为( )| A. | 84 | B. | 36 | C. | 54 | D. | 72 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com