
| ƽ���� | ��λ�� | ���� | |
| �� | 8 | 8 | 2 |
| �� | 8 | 8 | 2.2 |
| �� | 6 | 6 | 3 |
���� ��1�����ݷ��ʽ����λ���Ķ���ֱ���н�ɣ�
��2�����ݷ��ʽ�ȷֱ�����ķ���ٸ��ݷ�������弴����ԽСԽ�ȶ����ɵó��𰸣�
��3�����������Ȼ�����״ͼ���ó�����������ͼס������ڳ�������������ٸ��ݸ��ʹ�ʽ���ɵó��𰸣�
��� �⣺��1����ƽ������8��
��ķ����ǣ�$\frac{1}{10}$[��9-8��2+2��10-8��2+4��8-8��2+2��7-8��2+��5-8��2]=2��
�ѱ��˶�Ա����гɼ���С��������Ϊ��3��4��5��5��6��6��7��7��8��9������λ����$\frac{6+6}{2}$=6��
�ʴ�Ϊ��6��2��
��2���ķ����ǣ�$\frac{1}{10}$[��9-8��2+2��10-8��2+4��8-8��2+2��7-8��2+��5-8��2]=2��
�ҵķ����ǣ�$\frac{1}{10}$[2��9-8��2+2��10-8��2+2��8-8��2+3��7-8��2+��5-8��2]=2.2��
���ķ����ǣ�$\frac{1}{10}$[��9-6��2+��8-6��2+2��7-6��2+2��6-6��2+2��5-6��2+��4-6��2+��3-6��2]=3��
��S��2��S��2��S��2��
����˶�Ա�ijɼ����ȶ���
��3���������⻭ͼ���£�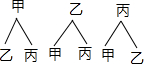
�߹���6����������ס������ڳ�������4�������
��ס������ڳ����ĸ�����$\frac{4}{6}$=$\frac{2}{3}$��
���� ���⿼���˷��ƽ��������λ���ͻ���״ͼ������ʣ�һ�����n�����ݣ�x1��x2����xn��ƽ����Ϊ$\overline{x}$����S2=$\frac{1}{n}$[��x1-x?��2+��x2-x?��2+��+��xn-x?��2]������ӳ��һ�����ݵIJ�����С������Խ������Խ��֮Ҳ����������=������������������֮�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 204��103 | B�� | 20.4��104 | C�� | 2.04��105 | D�� | 2.04��106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
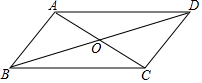 ��?ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AB=4��BD=10��sin��BDC=$\frac{3}{5}$����?ABCD�������24��
��?ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AB=4��BD=10��sin��BDC=$\frac{3}{5}$����?ABCD�������24���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
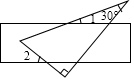 ֱ�����ǰ��ֱ����ͼ���ã�����1=20�㣬���2�Ķ���Ϊ��������
ֱ�����ǰ��ֱ����ͼ���ã�����1=20�㣬���2�Ķ���Ϊ��������| A�� | 60�� | B�� | 50�� | C�� | 40�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
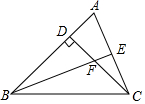 ��ͼ���ڡ�ABC�У�CD��AB���ϸߣ�BEΪ��ƽ���ߣ�����BFC=113�㣬���BCF�Ķ�����
��ͼ���ڡ�ABC�У�CD��AB���ϸߣ�BEΪ��ƽ���ߣ�����BFC=113�㣬���BCF�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
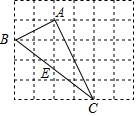 ��ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC������������ڸ���ϣ�����E��BC���е㣬��sin��CAE��ֵΪ��������
��ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC������������ڸ���ϣ�����E��BC���е㣬��sin��CAE��ֵΪ��������| A�� | 2 | B�� | $\frac{1}{2}$ | C�� | $\sqrt{5}$ | D�� | $\frac{{\sqrt{5}}}{5}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com