
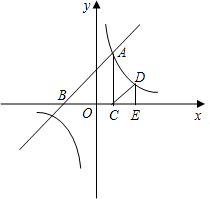
如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为 ,点A、D的坐标分别为(-4,0),(0,4). 动点P从A点出发,在AB边上匀速运动. 动点Q从点B出发,在折线BCD上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4). 动点P从A点出发,在AB边上匀速运动. 动点Q从点B出发,在折线BCD上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
【小题1】求出点C的坐标
【小题2】求S随t变化的函数关系式;
【小题3】当t为何值时,S有最大值?并求出这个最大值
【小题1】把y=4代入y=-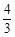 x+
x+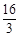 ,得x=1.
,得x=1.
∴C点的坐标为(1,4).
【小题2】当y=0时,-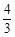 x+
x+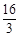 =0,
=0,
∴x=4.∴点B坐标为(4,0).
过点C作CM⊥AB于M,则CM=4,BM=3.
∴BC=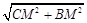 =
= =5.
=5.
∴sin∠ABC=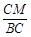 =
=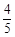 .
.
① 0<t<4时,过Q作QN⊥OB于N,
② 
则QN=BQ·sin∠ABC=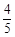 t.
t.
∴S= OP·QN=
OP·QN= (4-t)×
(4-t)×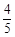 t =-
t =- t2+
t2+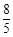 t(0<t<4). ……………2分
t(0<t<4). ……………2分
②当4<t≤5时,
连接QO,QP,过点Q作QN⊥OB于N.
同理可得QN=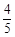 t.
t.
∴S= OP·QN=
OP·QN= ×(t-4)×
×(t-4)×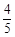 t.
t.
= t2-
t2-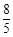 t(4<t≤5). …………………………….3分
t(4<t≤5). …………………………….3分
③当5<t≤6时,
连接QO,QP.
S= ×OP×OD=
×OP×OD= (t-4)×4.
(t-4)×4.
=2t-8(5<t≤6). ……………………………….4分
S随t变化的函数关系式是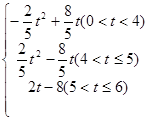 .
.
【小题3】①当0<t<4时,
∵- <0
<0
当t= =2时,
=2时,
S最大= =
=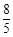 . ……………………………5分
. ……………………………5分
②当4<t≤5时, S= t2-
t2-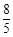 t,对称轴为t=-
t,对称轴为t=- =2,
=2,
∵ >0
>0
∴在4<t≤5时,S随t的增大而增大.
∴当t=5时,S最大= ×52-
×52-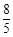 ×5=2. …………………………..6分
×5=2. …………………………..6分
③当5<t≤6时,
在S=2t-8中,∵2>0,∴S随t的增大而增大.
∴当t=6时,S最大=2×6-8=4. …………………………………………7分
∴综合三种情况,当t=6时,S取得最大值,最大值是4. ………………………8分
解析


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
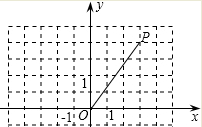 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′. | PP′ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 6 |
| x |
| 3 |
| 2 |
| 6 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com