
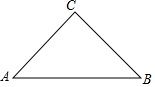
 如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为$\frac{5\sqrt{2}}{3}$.
如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为$\frac{5\sqrt{2}}{3}$. 分析 作DG⊥AE,先根据翻折变换的性质得到△DEF≌△BEF,再根据等腰三角形的性质及三角形外角的性质可得到∠AED=CDF,设CF=x,则DF=FB=4-x,根据勾股定理求出CF,可知tan∠AED=tanCDF,在Rt△ADG和Rt△EDG分别求出DG、EG,然后根据勾股定理即可得到结论.
解答 解:作DG⊥BE,
∵△DEF是△BEF翻折而成,
∴△DEF≌△BEF,∠B=∠EDF,
∵△ABC是等腰直角三角形,
∴∠EDF=45°,由三角形外角性质得∠CDF+45°=∠AED+45°,
∴∠AED=∠CDF,
∵CA=CB=4,CD=AD=2,
设CF=x,
∴DF=FB=4-x,
∴在Rt△CDF中,由勾股定理得,CF2+CD2=DF2,即x2+4=(4-x)2,
解得x=$\frac{3}{2}$,
∵∠A=45°,AD=2,
∴AG=DG=$\sqrt{2}$,
∵tan∠AED=tanCDF=$\frac{CF}{CD}$=$\frac{3}{4}$,
∴$\frac{DG}{EG}$=$\frac{3}{4}$,
∴$\frac{\sqrt{2}}{EG}$=$\frac{3}{4}$,
∴EG=$\frac{4\sqrt{2}}{3}$,
∴DE=BE=$\sqrt{D{G}^{2}+E{G}^{2}}$=$\frac{5\sqrt{2}}{3}$.
故答案为:$\frac{5\sqrt{2}}{3}$.
点评 本题考查的是图形翻折变换的性质、等腰直角三角形的性质、勾股定理、三角形外角的性质以及锐角三角函数的综合运用,涉及面较广,但难易适中.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
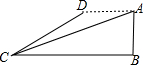 如图,飞机的高度AB=1000千米,从飞机上测得地面着陆点C的俯角为18°,飞机水平飞行一段距离后,到达D点,此时测得地面着陆点C的俯角为30°,求飞机飞行的距离AD的长(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,tan18°≈0.32)
如图,飞机的高度AB=1000千米,从飞机上测得地面着陆点C的俯角为18°,飞机水平飞行一段距离后,到达D点,此时测得地面着陆点C的俯角为30°,求飞机飞行的距离AD的长(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,tan18°≈0.32)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
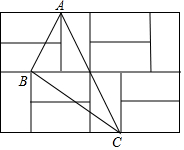 如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.
如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
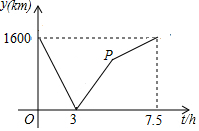 A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.
A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com