
��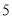 �֣���ͼ��һ�κ���
�֣���ͼ��һ�κ��� ��ͼ���뷴��������
��ͼ���뷴�������� ͼ����
ͼ����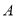 ��
��  ���㣬��
���㣬��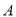 ������Ϊ
������Ϊ ��
��

��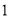 ����һ�κ����ͷ����������ı���ʽ��
����һ�κ����ͷ����������ı���ʽ��
�� ����
���� �������
�������

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�˽̰��ϲ��4�� ����ͼ�γ��� ��Ԫ���Ծ� ���ͣ������
�����ڼס������صĿͳ�����;ͣ��3����վ������Ʊ��һ������ ��������վ���Ʊ�۶���ͬ������____�ֲ�ͬ��Ʊ�ۣ�����____�ֳ�Ʊ.
10 20 ��������;����������վ���������˵��յ�վ�������վ. ��A��B��C��D��E��ʾ�����վ����Ҫ��ͬ��Ʊ�۵ij�Ʊ���Ա�ʾΪAB��AC��AD��AE��BC��BD��BE��CD��CE��DE��10�֣� ��Ϊ�����ij�Ʊ��ȻƱ��һ����������ͬ�� ��������Ҫ��10��2=20�ֲ�ͬ�ij�Ʊ.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ������
һ��ֱ��������ľ�壬����һ��ֱ�DZ�AB��1.5m�����Ϊ1.5m2���ס�����λľ���ֱ�ͼ�١��ڰ����ӹ���һ�����������森��˵���ĸ�����������ϴӹ���IJ��ƣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ������
��ͼ�����߳�Ϊ6cm��������ABCD�۵���ʹ��D����AB�ߵ��е�E�����ۺ�ΪFH����C����Q����EQ��BC���ڵ�G�����EBG���ܳ��� cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
�� �֣���ͼ�����ı���
�֣���ͼ�����ı���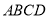 �У�
�У�  ƽ��
ƽ�� ��
��  ��
��  Ϊ
Ϊ ���е㣬����
���е㣬���� ��
�� ��
��  ��
��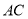 �ڵ�
�ڵ� ��
��
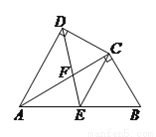
��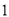 ����֤��
����֤��  ��
��
��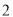 ����
���� ��
��  ����
���� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ��  ��
�� ��˫�����ϵ����㣬��
��˫�����ϵ����㣬��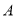 ����
����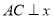 ���ڵ�
���ڵ� ����
���� �ڵ�
�ڵ� ����
���� �����Ϊ
�����Ϊ ��
�� 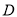 Ϊ
Ϊ ���е㣬��
���е㣬��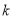 ��ֵΪ__________��
��ֵΪ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ����ƽ���ı��� �У�
��  ��
�� 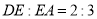 ��
��  ����
����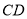 �ij��� ����
�ij��� ����

A.  B.
B.  C.
C.  D.
D. 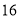
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�꼶��ѧ�²�ڶ�ʮ���� ������ ���ͣ���ѡ��
һ�������������ͼ��ͼ�����丩��ͼΪ�����Σ������������ı����Ϊ��������
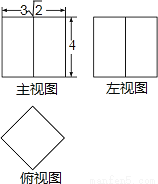
A. 66 B. 48 C. 48 +36 D. 57
+36 D. 57
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰����꼶�²���ѧ�������ཻ����ƽ���ߵ�Ԫ���� ���ͣ������
��ͼ��ʾ��ֱ��a��b��ֱ��c��ֱ��a��b�ֱ��ཻ�ڵ�A����B��AM��b������Ϊ��M������l=58�㣬���2= ___________ .
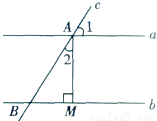
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com