
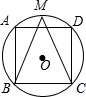
 如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$中点,连接BM,CM
如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$中点,连接BM,CM分析 (1)根据圆心距、弦、弧之间的关系定理解答即可;
(2)根据正方形的性质得出∠BOC的度数,进而得出答案.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=CD,
∴$\widehat{AB}$=$\widehat{CD}$,
∵M为$\widehat{AD}$中点,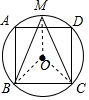
∴$\widehat{AM}$=$\widehat{DM}$,
∴$\widehat{AB}$+$\widehat{AM}$=$\widehat{CD}$+$\widehat{DM}$,即$\widehat{BM}$=$\widehat{CM}$,
∴BM=CM;
(2)解:连接MO,BO,CO,
∵正方形ABCD内接于⊙O,
∴∠BOC=90°,
∵$\widehat{BM}$=$\widehat{CM}$,
∴∠BOM=∠COM=135°.
点评 本题考查的是正方形的性质、弧长的计算、圆心距、弦、弧之间的关系,掌握圆心距、弦、弧之间的关系定理是解题的关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:解答题
| 组号 | 分组 | 频数 |
| 一 | 9.6≤x<9.7 | 1 |
| 二 | 9.7≤x<9.8 | 2 |
| 三 | 9.8≤x<9.9 | a |
| 四 | 9.9≤x<10 | 8 |
| 五 | x=10 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
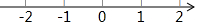 如图所示,数轴上的点A,B,C依次表示三个实数:1$\frac{1}{2}$,-1$\frac{1}{2}$,$\sqrt{3}$.
如图所示,数轴上的点A,B,C依次表示三个实数:1$\frac{1}{2}$,-1$\frac{1}{2}$,$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com