
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
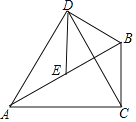
(1)求证:△ADE≌△CDB;
(2)若BC=1,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据等边三角形的性质,三边相等,各角为60°,与直角三角形的性质,和斜边上的中线等于斜边的一半的定理,可得AE=DE=DB=BC,∠DBC=∠AED=120°,即可证明.
(2)根据轴对称的性质和两点之间线段最短的公理,做出B点关于AC的对称点B′, 连接B′E,通过计算求出即可.
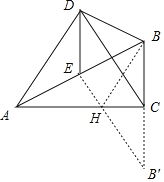
如图:
(1)在Rt△ABC中,∠ACB=90°,∠BAC=30°,
∴BC=![]() AB.∠ABC=60°.
AB.∠ABC=60°.
∵E为AB边的中点,
∴AE=BE,
∵△BDE是等边三角形,
∴BE=BD=DE,∠DBE=∠DEB=60°,
∴AE=DE=DB=BC,∠DBC=∠AED=120°,
∴△ADE≌△CDB(SAS).
(2)作点B关于AC的对称点B′,连接B′E交AC于点H,
此时BH=B′H,B′E=B′H+HE=BH+HE最小.
∵BC=1,BB′=2,∴B′H=![]() .
.
答:这个最小值为![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,DE分别是边AB、AC上的点,且AD=CE,则∠ADC+∠BEA=( )
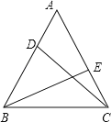
A.180°B.170°C.160°D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.

(1)求点B的坐标;
(2)在x轴上找一点D,连接BD使得△ABD与△ABC相似(不包括全等),并求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点P是BC延长线上一点,连结PD并延长交BA延长线于点E.记△ABP的面积为S1,△ECP的面积为S2,则S1与S2的大小关系是( )
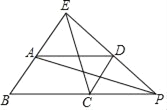
A. S1=S2 B. S1>S2 C. S1<S2 D. 都可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0).
(1)当t=1时,KE=_____,EN=_____;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
(4)当t为何值时,△PKB是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )

A. sinα=cosα B. tanC=2 C. sinβ=![]() D. tanα=1
D. tanα=1
查看答案和解析>>
科目:初中数学 来源: 题型:
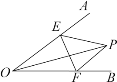
【题目】如图,∠AOB = 30°,点P是∠AOB内任意一点,且OP = 7,点E和点F分别是射线OA和射线OB上的动点,则△PEF周长的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的钢架中,∠A=18°,焊上等长的钢条P1P2,P2P3,P3P4,P4P5…来加固钢架.∠P5P4B的度数是( )
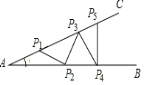
A.80°B.85°C.90°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内接于⊙O,E为弧CD上任意一点,连接DE,AE.
(1)求∠AED的度数;
(2)如图②,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
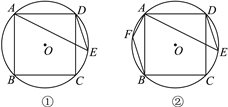
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com