
 如图,已知锐角三角形ABC的外角∠ACD的平分线CP与内角∠ABC的平分线相交于P,连接AP,若∠BPC=40°,求∠CAP的度数?
如图,已知锐角三角形ABC的外角∠ACD的平分线CP与内角∠ABC的平分线相交于P,连接AP,若∠BPC=40°,求∠CAP的度数?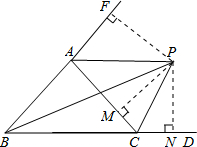
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
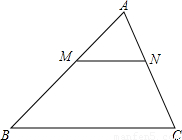
 A1MN与四边形BCNM重叠部分的面积为y,当x为何值时,y最大,最大值为多少.
A1MN与四边形BCNM重叠部分的面积为y,当x为何值时,y最大,最大值为多少.查看答案和解析>>
科目:初中数学 来源:鼎尖助学系列—同步练习(数学 八年级下册)、函数及其图象 画相似图形 题型:044
| |||||||||||
查看答案和解析>>
科目:初中数学 来源:第27章《二次函数》中考题集(33):27.3 实践与探索(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com