
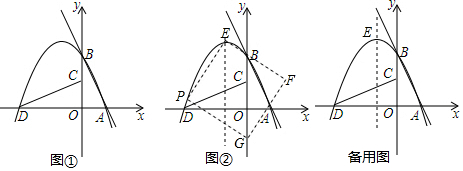
���� ��1������ֱ��l�Ľ���ʽ�ó�A��B�����꣬�ٸ�����ת�����ʵó�D�����꣬Ȼ���ô���ϵ������������߽���ʽ��
��2�����N������꣬�������ú���ʾ��ʾ��ͬʱ��ʾ��M�����꣬��MN�ij���ΪN����M���������֮��ó�MN�ij�����N�������Ķ��κ����������䷽�������ֵ��
��3����Ȼ��G����y���Ϻ�F����y�����������������ÿ������з��̽�����⣮
��� �⣺��1����ֱ��l��y=-2x+4��x���ڵ�A����y���ڵ�B��
��A��2��0����B��0��4����
�߽���AOB�Ƶ�O��ʱ����ת90��õ���COD��
��D��-4��0����C��0��2����
�����A��B��D��������h�Ľ���ʽΪ��y=a��x+4����x-2����
��B���������ɵã�4=a��0+4����0-2����
��a=-$\frac{1}{2}$��
��������h�Ľ���ʽΪy=-$\frac{1}{2}$x2-x+4��
��2����D��-4��0����C��0��2����
��ֱ��CD�Ľ���ʽΪy=$\frac{1}{2}$x+2��
��N��������n��-$\frac{1}{2}$n2-n+4����
��M��������n��$\frac{1}{2}n+2$����
��MN=yN-yM=-$\frac{1}{2}{n}^{2}-\frac{3}{2}n+2$=-$\frac{1}{2}$��n+$\frac{3}{2}$��2+$\frac{25}{8}$��
�൱n=-$\frac{3}{2}$ʱ��MN������ֵΪ$\frac{25}{8}$��
��3����G����y���ϣ���ͼ��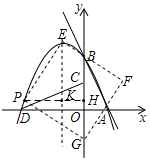
��PH��y����H���������߶Գ�����K��
�ڡ�PKE�͡�GHP�У�
$\left\{\begin{array}{l}{��EPK=��PGH}\\{PE=GP}\\{��PEK=��GPH}\end{array}\right.$��
���PKE�ա�GHP��
��PK=GH��EK=PH��
��y=-$\frac{1}{2}$x2-x+4=-$\frac{1}{2}$��x+1��2+$\frac{9}{2}$��
��E��-1��$\frac{9}{2}$����
��P��m��-$\frac{1}{2}{m}^{2}-m+4$������
EK=yE-yP=$\frac{9}{2}$+$\frac{1}{2}{m}^{2}+m-4$=$\frac{1}{2}{m}^{2}+m+\frac{1}{2}$��
PH=-m��
��$-m=\frac{1}{2}{m}^{2}+m+\frac{1}{2}$��
��$m=-2��\sqrt{3}$��
��P���������-2-$\sqrt{3}$��$\frac{5}{2}-\sqrt{3}$����-2+$\sqrt{3}$��$\frac{5}{2}+\sqrt{3}$����
��F����y���ϣ���ͼ��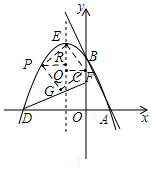
��PR�������߶Գ�����R��FQ�������߶Գ�����Q��
���PER�ա�EFQ��
��ER=FQ��
��yE-yP=-xE��
��$\frac{1}{2}{m}^{2}+m+\frac{1}{2}$=1��
��m=-1-$\sqrt{2}$��m=-1+$\sqrt{2}$���ᣩ��
��P���������-1-$\sqrt{2}$��$\frac{7}{2}$����
��������������Ҫ���P���������������ֱ�Ϊ����-2-$\sqrt{3}$��$\frac{5}{2}-\sqrt{3}$������-2+$\sqrt{3}$��$\frac{5}{2}+\sqrt{3}$����-1-$\sqrt{2}$��$\frac{7}{2}$����
���� �����Ƕ��κ����ۺ��⣬��Ҫ������һ�κ���ͼ��������������������ϵ��������κ�������ʽ������������֮���ʾ��ֱ�����߶εij��ȣ������䷽������κ�����ֵ�������ε����ʡ�ȫ�������ε��ж������ʡ���һԪ���η��̵��ڶ�֪ʶ�㣬�ۺ���ǿ���ѶȽϴ��ڣ�3���ʣ����������ε�����������ȫ�������Σ��Ӷ��ó��߶���ȶ��г������ǽ��Ĺؼ���Ҫ�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����������������Ͷ�����ڣ�������ڻ���ͼ��ÿһ��С�����������ǵȿ��ܵģ�Ͷ������1�Σ�����ͼ����Ӱ���ֵĸ����ǣ�������
��ͼ����������������Ͷ�����ڣ�������ڻ���ͼ��ÿһ��С�����������ǵȿ��ܵģ�Ͷ������1�Σ�����ͼ����Ӱ���ֵĸ����ǣ�������| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{3}{8}$ | D�� | $\frac{5}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ab2�Ĵ�����2 | B�� | 1�ǵ���ʽ | ||
| C�� | $\frac{-3{a}^{3}c}{7}$ϵ����-3 | D�� | ����ʽa+b2�Ĵ�����3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 13Ԫ | B�� | 12Ԫ | C�� | 15Ԫ | D�� | 16Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��� | B�� | ֱ�� | C�� | �۽� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com