
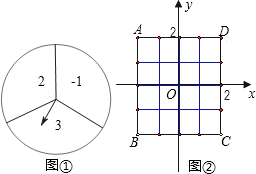
 的数字为纵坐标).
的数字为纵坐标). ?若存在,指出其中的一种平移方式;若不存在,请说明理由.
?若存在,指出其中的一种平移方式;若不存在,请说明理由.
 ;
; ,
, ,可得P点落在正方形ABCD面上(含正方形内和边界)的有6种情况,继而求得答案.
,可得P点落在正方形ABCD面上(含正方形内和边界)的有6种情况,继而求得答案.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
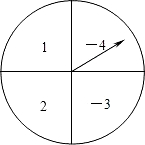 如图所示,有一个可以自由转动的圆形转盘,被平均分成四个扇形,四个扇形内分别标有数字1、2、-3、-4、若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为a、b(若指针恰好指在分界线上,则该次不计,重新转动一次,直至指针落在扇形内).
如图所示,有一个可以自由转动的圆形转盘,被平均分成四个扇形,四个扇形内分别标有数字1、2、-3、-4、若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为a、b(若指针恰好指在分界线上,则该次不计,重新转动一次,直至指针落在扇形内).查看答案和解析>>
科目:初中数学 来源: 题型:
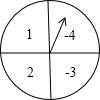 转动一次,直至指针落在扇形内).
转动一次,直至指针落在扇形内).查看答案和解析>>
科目:初中数学 来源: 题型:
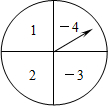 直至指针落在扇形内).
直至指针落在扇形内).查看答案和解析>>
科目:初中数学 来源: 题型:
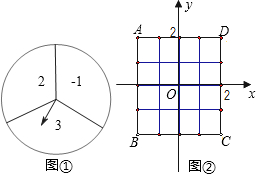 的数字为纵坐标).
的数字为纵坐标).| 2 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com