
【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
【答案】B
【解析】
过点C作CD⊥BF,交FB的延长线于点D,易证△ACE≌△BCD,根据全等三角形的对应边相等,即可证得AF+BF=2CE,由此即可解决问题。
(1)证明:如图1,过点C作CD⊥BF,交FB的延长线于点D,
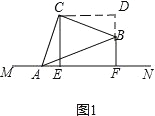
∵CE⊥MN,CD⊥BF,
∴∠CEA=∠D=90°,
∵CE⊥MN,CD⊥BF,BF⊥MN,
∴四边形CEFD为矩形,
∴∠ECD=90°,
又∵∠ACB=90°,
∴∠ACB-∠ECB=∠ECD-∠ECB,
即∠ACE=∠BCD,
又∵△ABC为等腰直角三角形,
∴AC=BC,
在△ACE和△BCD中,
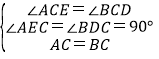 ,
,
∴△ACE≌△BCD(AAS),
∴AE=BD,CE=CD,
又∵四边形CEFD为矩形,
∴四边形CEFD为正方形,
∴CE=EF=DF=CD,
∴AF+BF=AE+EF+BF
=BD+EF+BF
=DF+EF
=2CE,
∵CE=3,BF=2,
∴AF=6-2=4.
故选B.


科目:初中数学 来源: 题型:
【题目】【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,AC的垂直平分线MN交AB于D,交AC于E.

(1)若∠A=40°,求∠BCD的度数;
(2)若AE=5,△BCD的周长17,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,在平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(3,0),

(1)在图中作出线段AB以二四象限的角平分线为对称轴的对称线段CD,并直接写出四边形ABDC的面积为 ;
(2)若点C为格点(横纵坐标均为整数),且AB⊥OC,且AB=OC,作出线段OC;并写出C点坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )

A. 9 B. ![]() C. 27 D.
C. 27 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N.设△BPQ,△DKM,△CNH的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( )

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)填空:∠CAM=__________度;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com