
【题目】如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足 ![]() +(b2﹣16)2=0.
+(b2﹣16)2=0. 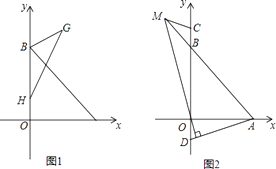
(1)求A、B两点的坐标,∠OAB的度数;
(2)如图1,已知H(0,1),在第一象限内存在点G,HG交AB于E,使BE为△BHG的中线,且S△BHE=3,
①求点E到BH的距离;
②求点G的坐标;
(3)如图2,C,D是y轴上两点,且BC=OD,连接AD,过点O作MN⊥AD于点N,交直线AB于点M,连接CM,求∠ADO+∠BCM的值.
【答案】
(1)解:∵ ![]() +(b2﹣16)2=0,
+(b2﹣16)2=0,
∴a﹣b=0,b2﹣16=0,
解得:b=4,a=4或b=﹣4,a=﹣4,
∵A点在x轴正半轴,B点在y轴正半轴上,
∴b=4,a=4,
∴A(4,0),B(0,4),
∴OA=OB=4,
∴∠OAB=45°
(2)解:①如图1,作EF⊥y轴于F,
∵B(0,4),H(0,1),
∴BH=OB﹣OH=4﹣1=3,
∵OA=OB=4,
∴△OAB为等腰直角三角形,
∴∠OBA=∠OAB=45°,
∴△BFE为等腰直角三角形,
∴BF=EF=2,
∴OF=OB﹣BF=4﹣1=3,
∴E(2,3),
∴E(2,3)为GH的中点,
∵S△BHE=3,
∴ ![]() BH×EF=3,即
BH×EF=3,即 ![]() ×3×EF=3,
×3×EF=3,
∴EF=2,
故点E到BH的距离为2.
②设G(m,n),则
∵BE为△BHG的中线,
∴ ![]() ,
, ![]() ,
,
解得m=4,n=5,
∴G点坐标为(4,5)
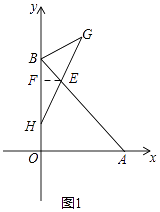
(3)解:如图2,过点B作BK⊥OC,交MN于点K,则∠KBO=∠DOA,
∵MN⊥AD,
∴∠DON+∠NOA=90°,
∴∠3+∠NOA=90°,
∵∠NOA+∠1=90°,
∴∠3=∠1,
在△KOB和△OAD中,
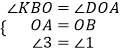 ,
,
∴△KOB≌△OAD(ASA),
∴KB=OD,∠2=∠7,
∵BC=OD,
∴KB=BC,
∵OB=OA,∠BOA=90°,
∴∠OBA=45°,
∴∠9=∠8=45°,
在△MKB和△MCB中,
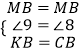 ,
,
∴△MKB≌△MCB(SAS),
∴∠6=∠5,
∵∠7+∠6=180°,
∴∠2+∠5=180°,即∠ADO+∠BCM=180°.
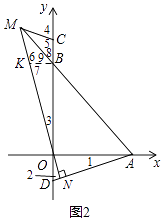
【解析】(1)根据非负数的性质,得出关于a、b的方程组,求得a、b即可得到A、B两点的坐标,最后利用等腰三角形的性质得出∠OAB的度数;(2)作EF⊥y轴于F,构造等腰直角三角形BEF,进而求出E点坐标,利用△BHE的面积即可得到点E到BH的距离;设G(m,n),根据BE为△BHG的中线,求得点G坐标即可;(3)过点B作BK⊥OC,交MN于点K,然后证明△OBK≌△OAD、△MKB≌△MCB,从而可证明∠ADO+∠BCM=180°.
【考点精析】掌握等腰直角三角形和三角形的面积是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;三角形的面积=1/2×底×高.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将代数式4a2b+3ab2﹣2b2+a3按a的升幂排列的是( )
A.﹣2b3+3ab2+4a2b+a3
B.a3+4a2b+3ab2﹣2b3
C.4a2b+3ab2﹣2b3+a3
D.4a2b+3ab2+a3﹣2b3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线AB 与y轴交于点A,与x轴交于点B,与双曲线y= ![]() (x>0)交于点C(1,6)和点D(3,n).作CE⊥y轴于E,DF⊥x轴于F.
(x>0)交于点C(1,6)和点D(3,n).作CE⊥y轴于E,DF⊥x轴于F.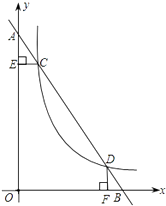
(1)求出m、n的值;
(2)求出直线AB的解析式;
(3)是否有△AEC≌△DFB,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,一只蚂蚁从原点出发,先向右爬行了4个单位长度到达点A,再向右爬行了2个单位长度到达点B,然后又向左爬行了10个单位长度到达点C.
(1)画出数轴,并在数轴上表示出A、B、C三点;
(2)根据点C在数轴上的位置,点C可以看作是蚂蚁从原点出发,向哪个方向爬行了几个单位长度得到的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com