
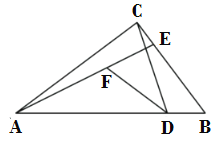
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,
边上,![]() ,点
,点![]() 在
在![]() 边上,
边上,![]() ,点
,点![]() 为
为![]() 上一点,
上一点,![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为___________.
的长为___________.
【答案】4
【解析】
过点F作FG⊥FD交AB于点G,设∠BCD=α,∠BAE=β,AD=x,根据等对等角可推出2α+2β=90°,从而证出∠FGD=∠B,然后等角的正弦值相等即可求出DG=![]() ,从而求出AG,再根据等角对等边可得GF=AG,最后根据勾股定理列出方程即可求出结论.
,从而求出AG,再根据等角对等边可得GF=AG,最后根据勾股定理列出方程即可求出结论.
解:过点F作FG⊥FD交AB于点G
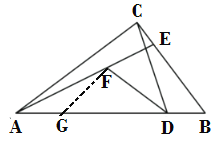
设∠BCD=α,∠BAE=β,AD=x
则∠ADF=2α,∠B=2β,AC=AD=x,AB=AD+BD=x+1
∴∠ADC=∠ACD=∠ACB-∠BCD=90°-α
∵∠ADC=∠BCD+∠B
∴90°-α=α+2β
整理可得:2α+2β=90°
在Rt△DFG中,∠FGD=90°-∠FDG=90°-2α=2β
即∠FGD=∠B
∵sin∠B=![]() ,sin∠FGD=
,sin∠FGD=![]()
∴![]()
解得:DG=![]()
∴AG=AD-DG=![]()
∵∠FGD=2β,∠BAE=β
∴∠GFA=∠FGD-∠BAE=β=∠BAE
∴GF=AG
在Rt△DFG中,GF2+DF2=DG2
即AG2+4=(x-AG)2
整理,得x2-2x·AG=4
∴x2-2x·![]() =4
=4
整理,得x2-4x=0
解得:x1=4,x2=0(不符合实际,舍去)
即AD=4
故答案为:4.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为![]() 分)、
分)、![]() 分)、
分)、![]() 分)、
分)、![]() 分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
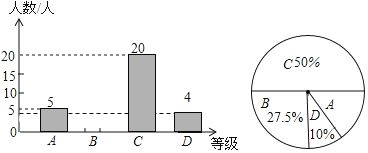
其中组![]() 的期末数学成绩如下
的期末数学成绩如下
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请补全条形统计图;
(2)这部分学生的期末数学成绩的中位数是 ,![]() 组的期末数学成绩的众数是 ;
组的期末数学成绩的众数是 ;
(3)这个学校九年级共有学生![]() 人,若分数为
人,若分数为![]() 分(含
分(含![]() 分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有善行者行一百步,不善行者行六十步”(出自《九章算术》)意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步,假定两者步长相等,据此回答以下问题:
(1)今不善行者先行一百步,善行者追之,不善行者再行六百步,问孰至于前,两者几何步隔之?即:走路慢的人先走100步,走路快的人开始追赶,当走路慢的人再走600步时,请问谁在前面,两人相隔多少步?
(2)今不善行者先行两百步,善行者追之,问几何步及之?即:走路慢的人先走200步,请问走路快的人走多少步才能追上走路慢的人?
查看答案和解析>>
科目:初中数学 来源: 题型:
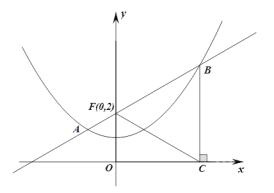
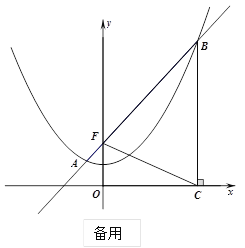
【题目】如图,已知抛物线![]() 过点
过点![]() ,过定点
,过定点![]() 的直线
的直线![]() :
:![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 在x轴上运动,连接
在x轴上运动,连接![]() ,作
,作![]() 的垂直平分线与过点D作x轴的垂线交于点
的垂直平分线与过点D作x轴的垂线交于点![]() ,判断点
,判断点![]() 是否在抛物线
是否在抛物线![]() 上,并证明你的判断;
上,并证明你的判断;
(3)若![]() ,设
,设![]() 的中点为
的中点为![]() ,抛物线上是否存在点
,抛物线上是否存在点![]() ,使得
,使得![]() 周长最小,若存在求出周长的最小值,若不存在说明理由;
周长最小,若存在求出周长的最小值,若不存在说明理由;
(4)若![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在求出点
,若存在求出点![]() 的坐标,若不存在说明理由.
的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃3、4、5三张牌,小明先抽一张,记录后放回,小刚再从3张中随机抽一张,若两张牌上的数字之积是奇数,则小明看电影,否则小刚看电影,乙的方案公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() ;
;

(1)如图1,求抛物线的解析式;
(2)如图2,点![]() 在第四象限的抛物线上,连接
在第四象限的抛物线上,连接![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 在
在![]() 上,连接
上,连接![]() 、
、![]() ,
,![]() ,
,![]() ,求
,求![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次购进20件A商品,40件B商品,共用了1980元.脱销后,在进价不变的情况下,第二次购进40件A商品,20件B商品,共用了1560元.商品A的售价为每件30元,商品B的售价为每件60元.
(1)求A,B两种商品每件的进价分别是多少元?
(2)为了满足市场需求,需购进A,B两种商品共1000件,且A种商品的数量不少于B种商品数量的3倍,请你设计进货方案,使这1000件商品售完后,商场获利最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
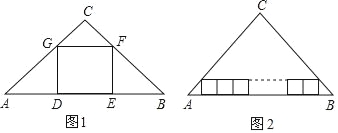
【题目】在△ABC中,∠C=90°,AC=4,BC=3,如图1,四边形DEFG为△ABC的内接正方形,则正方形DEFG的边长为_____.如图2,若三角形ABC内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一驴友分三次从![]() 地出发沿着不同线路(
地出发沿着不同线路(![]() 线、
线、![]() 线、
线、![]() 线)去
线)去![]() 地,在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种.他涉水行走4小时的路程与攀登6小时的路程相等;
地,在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种.他涉水行走4小时的路程与攀登6小时的路程相等;![]() 线、
线、![]() 线路程相等,都比
线路程相等,都比![]() 线路程多
线路程多![]() ;
;![]() 线总时间等于
线总时间等于![]() 线总时间的一半;他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完
线总时间的一半;他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完![]() 线;在
线;在![]() 线中穿越丛林、涉水行走和攀登所用时间分别比
线中穿越丛林、涉水行走和攀登所用时间分别比![]() 线上升了
线上升了![]() .若他用了
.若他用了![]() 小时穿越丛林、
小时穿越丛林、![]() 小时涉水行走和
小时涉水行走和![]() 小时攀登走完
小时攀登走完![]() 线,且
线,且![]() 都为正整数,则
都为正整数,则![]() _____.
_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com