
����Ŀ�������ⱳ����
��֪��l1��l2��l3��l4��ƽ����l1��l2��l2��l3��l3��l4֮��ľ���ֱ�Ϊd1��d2��d3����d1=d3=1��d2=2�����ǰ��ĸ�����ֱ���l1��l2��l3��l4������ƽ�����ϵ��ı��γ�Ϊ�������ı��Ρ���

������̽����
��1����ͼ1��������ABCDΪ�������ı��Ρ�����������ABCD�ı߳�Ϊ ��
��2������ABCDΪ�������ı��Ρ����䳤����=2��1�������ABCD�Ŀ���
��������չ��
��3����ͼ1��EG��������ABCD�Ķ���D�Ҵ�ֱl1�ڵ�E���ֱ�l2��l4�ڵ�F��G������AEG�Ƶ�A˳ʱ����ת30�㣬�õ���AE��D������ͼ2������D����ֱ��l3�ϣ���AD��Ϊ����E��D�����������AB��C��D�䣬ʹB��C�䣬�ֱ���ֱ��l2��l4�ϣ�������AB��C��D��ı߳���
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3��
����3��![]()
��������
�����������1��������֪�ó���AED�ա�DGC��AAS�������ɵó�AE���Լ������εı߳���
��2����ͼ2����B��BE��L1�ڵ�E�������ӳ�BE��L4�ڵ�F����BE=1��BF=3�����ı���ABCD�Ǿ��Σ���ABC=90������ABE+��FBC=90����������ABE+��EAB=90�����õ���FBC=��EAB��Ȼ��������ۣ���þ��εĿ���
��3�����ȹ���E����ON��ֱ��l1�ֱ�l1��l2�ڵ�O��N����AEO=30��������ED��N=60���������AE=1��EO��EN��ED��ij��������ɹ��ɶ�����֪���εı߳���
�⣺��1����l1��l2��l3��l4����AED=90�����DGC=90����
���ı���ABCDΪ�����Σ�
���ADC=90����AD=CD��
�ߡ�ADE+��2=90����
���1+��2=90����
���1=��ADE��
��l3��l4
���1=��DCG��
��ADE=��DCG��
����AED����DGC��
 ��
��
���AED�ա�GDC��AAS����
��AE=GD=1��ED=GC=3��
��AD=![]() =
=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����ͼ2����B��BE��L1�ڵ�E�������ӳ�BE��L4�ڵ�F��
��BE=1��BF=3��
���ı���ABCD�Ǿ��Σ�
���ABC=90����
���ABE+��FBC=90����
�ߡ�ABE+��EAB=90����
���FBC=��EAB��
��AB��BCʱ��AB=![]() BC��
BC��
��AE=![]() BF=
BF=![]() ��
��
��AB=![]() =
=![]() ��
��
��ͼ3��AB��BCʱ��
ͬ���ɵã�BC=![]() ��
��
�����εĿ�Ϊ��![]() ��
��![]() ��
��
��3����ͼ4����E����ON��ֱ��l1�ֱ�l1��l4�ڵ�O��N��
�ߡ�OAE��=30��������E��FN=60��
��AE��=AE=1��
��E��O=![]() ��E��N=
��E��N=![]() ��E��D��=
��E��D��=![]() ��
��
�ɹ��ɶ�����֪���εı߳�Ϊ��![]() =
=![]() =
=![]() ��
��






 �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���α�1.4������һ�����⣺
����4����һ����22cm����˿��
��1���ܷ�Χ�������30cm2�ľ��Σ�
��2���ܷ�Χ�������32cm2�ľ��Σ�
�ݴˣ�һλͬѧ������⣺���������22cm����˿�ܷ�Χ��������ľ��Σ�����Χ�ɣ����������ֵ��������Χ�ɣ���˵�����ɣ���������ɸ�ͬѧ��������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɭ���ǵ���֮�Σ�ÿ����Ϊ�����ṩ��Լ28.3�ڶֵ��л��28.3�ڶ��ÿ�ѧ��������ʾΪ�� ��
A��28.3��107 B��2.83��108
C��0.283��1010 D��2.83��109
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ���ǣ� ��
A��4a��3a=1 B��aa2=a3
C��3a6��a3=3a2 D����ab2��2=a2b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͨ�����������ϣ����Կ���һЩ��������Ĺ��ɣ�������2015��9�·ݵ������ƣ�
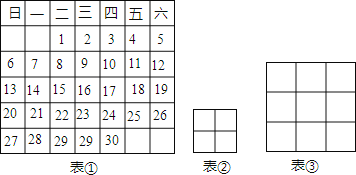
��1���ڱ����У�����ѡ�������������2��2�������ο�����Ȧ��2��2�������������߽�����ˣ���������磺�������ο�Ȧ��4��5��11��12�ĸ�����Ȼ�����ǽ�����ˣ����������4��12��5��11=��7��5��11��4��12=7�������ñ����������ο�����Ȧ��2��2�������������Ƚ�����ˣ���������г���ʽ����������ѡ������һ����ʽ���ɣ���
��2�����ñ����������ο�����Ȧ��2��2�����У��������Ƚ�����ˣ���������������Ͻǵ�����Ϊn���ú�n��ʽ�ӱ�ʾ��������λ�õ����֣��г���ʽ����������ѡ������һ����ʽ���ɣ���
��3����ѡ�������������3��3�������η�������Ȧ��3��3�������������η����ĸ���λ���ϵ�4�����Ƚ�����ˣ���������㷢����ʲô����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AD=5��AB=4����E��F��ֱ��AD�ϣ����ı���BCFEΪ���Σ����߶�EF���е�Ϊ��M�����߶�AM�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и�����Ϊ���ߵ��������в���ֱ�������ε���
A. 9��12��15 B. 41��40��9 C. 25��7��24 D. 6��5��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪1cm3��������ԼΪ0.00009g���ÿ�ѧ��������ʾ1cm3����������____________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ԷС���ڹ滮���ʱ����������¥��֮�䣬����һ�����Ϊ900ƽ���ľ����̵أ����ҳ��ȿ���10�ף����̵صĿ�Ϊx�ף��������⣬���з���Ϊ�� ��
A��x��x��10��=900
B��x��x+10��=900
C��10��x+10��=900
D��2[x+��x+10��]=900
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com