
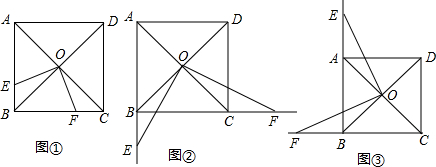
���� ��1����ͼ�ڣ����������ε����ʵõ�BC=$\frac{\sqrt{2}}{2}$AC��ͨ��ȫ�������Ρ�EOB�ա�FOC��ASA�������ʵõ���BE=CF������BC=CF+BF=BE+BF����BE-BF=$\frac{\sqrt{2}}{2}$AC��
��ͼ�ڣ����˼·ͬ�ϣ�
��2����AC=4$\sqrt{2}$�����BC=4��OC=OB=2$\sqrt{2}$����ֱ�������ε������ʽ���S��BOC=4������S��COF=1�����CF���������BF��ֵ������ͼ�ٺ�ͼ�ڷ����������⣮
��� �⣺��1����ͼ�ڣ�BF-BE=$\frac{\sqrt{2}}{2}$AC���������£�
���ı���ABCD�������Σ�
��OB=OC����EBO=��FCO=135�㣬��BOC=90��
�ߡ�EOF=90�㣬
���EOB=��FOC��
���ڡ�BOE���COF�У�$\left\{\begin{array}{l}{��EBO=��FCO}\\{OB=OC}\\{��BOE=��COF}\end{array}\right.$��
���BOE�ա�COF��ASA����
��BE=CF��
��BF=BC+CF=BC+BE����BF-BE=BC��
���ı���ABCD�������Σ�
��BC=$\frac{\sqrt{2}}{2}$AC��
��BF-BE=$\frac{\sqrt{2}}{2}$AC��
��ͼ�ۣ�BE-BF=$\frac{\sqrt{2}}{2}$AC���������£�
���ı���ABCD�������Σ�
��OB=OA����FBO=��EAO=135�㣬��BOA=90��
�ߡ�EOF=90�㣬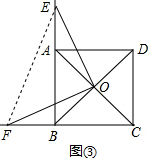
���FOB=��EOA��
���ڡ�BOF���AOE�У�$\left\{\begin{array}{l}{��FBO=��EAO}\\{OB=OA}\\{��FOB=��EOA}\end{array}\right.$��
���BOF�ա�AOE��ASA����
��BF=AE��
��BE=AB+AE=BC+BF����BE-BF=BC��
���ı���ABCD�������Σ�
��BC=$\frac{\sqrt{2}}{2}$AC��
��BE-BF=$\frac{\sqrt{2}}{2}$AC��
��2����AC=4$\sqrt{2}$��
��OC=OB=$\frac{1}{2}$AC=2$\sqrt{2}$��BC=4��
��S��BOC=$\frac{1}{2}$OB•OC=$\frac{1}{2}$��2$\sqrt{2}$��2$\sqrt{2}$=4��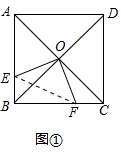
��ͼ�ۣ�����EF��
��S��COF=1��S��BOC=4��
��ͼ�۵���������ڣ�
��ͼ�٣�����EF��
��S��COF=1��S��BOC=4��
��BF��CF=3��1��
��BF=3��CF=1��
������֪��BE=CF=1��
��EF=$\sqrt{B{F}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$��
��ͼ�ڣ�����EF��
��S��COF=1��S��BOC=4��
��BF��CF=5��1��
��BF=5��CF=1��
������֪��BE=CF=1��
��EF=$\sqrt{B{F}^{2}+B{E}^{2}}$=$\sqrt{{5}^{2}+{2}^{2}}$=$\sqrt{26}$��
����������EF�ij�����$\sqrt{10}$��$\sqrt{26}$��
�ʴ��ǣ�4��$\sqrt{10}$��$\sqrt{26}$��
���� ���⿼�����ı����ۺ��⣬��������У��ۺ�������ȫ�������ε��ж������ʡ������ε������Լ����ɶ�����Ӧ�ã�ע�⣬���2���⣬Ҫ�������ۣ��Է�©�⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��5 | B�� | x��3 | C�� | x��3 | D�� | x��3��x��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com