
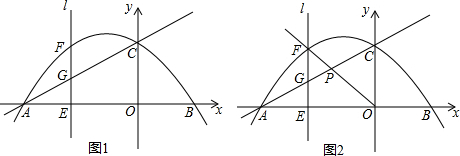
分析 (1)将B(4,0)代入抛物线的解析式可求得a的值,从而得到抛物线的解析式,然后由抛物线的解析式可求得A、C的坐标,接下来,依据待定系数法可求得AC的解析式;
(2)由E(m,0)可知F(m,-$\frac{1}{8}$m2-$\frac{1}{2}m$+4),G(m,$\frac{1}{2}$m+4).从而得到FG与m的函数关系式,然后依据配方法求得FG的最大值,以及m的取值即可;
(3)先证明△PEG∽△POC,由相似三角形的性质可求得FG=2,由(2)可知此时m的取值
解答 解:(1)∵将B(4,0)代入抛物线的解析式得:16a-2+4=0,解得:a=-$\frac{1}{8}$,
∴抛物线的解析式为y=-$\frac{1}{8}$x2-$\frac{1}{2}x+4$.
∵令y=0得;-$\frac{1}{8}$x2-$\frac{1}{2}x+4$=0,解得;x1=-8,x2=4,
∴A(-8,0).
∵令x=0得:y=4,
∴C(0,4).
设直线AC的解析式为y=kx+b
∵将点A、C的坐标代入得:$\left\{\begin{array}{l}{b=4}\\{-8k+b=0}\end{array}\right.$,解得:k=$\frac{1}{2}$,b=4,
∴直线AC的解析式为y=$\frac{1}{2}x+4$.
(2)∵点E的坐标为(m,0),
∴点F的坐标为(m,-$\frac{1}{8}$m2-$\frac{1}{2}m$+4),G(m,$\frac{1}{2}$m+4).
∴FG=-$\frac{1}{8}$m2-$\frac{1}{2}m$+4-($\frac{1}{2}$m+4)=$-\frac{1}{8}$m2-m=-$\frac{1}{8}$(m+4)2+2.
∴当m=-4时,FG有最大值,最大值为2.
(3)∵FG∥OC,
∴△PEG∽△POC.
∴$\frac{FG}{CO}=\frac{EP}{OP}$.
∴$\frac{FG}{OC}=\frac{1}{2}$时,FP:PO=1:2.
∴$\frac{FG}{4}=\frac{1}{2}$.
∴FG=2.
由(2)可知当m=-4时,FG有最大值,最大值为GF=2.
∴m=-4.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数、一次函数的解析式、配方法求二次函数的最大值、相似三角形的性质和判定,求得FG与m的函数关系式是解题的关键.


科目:初中数学 来源: 题型:解答题
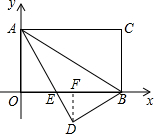 如图所示,已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点C的坐标为(8,4),将△ABC沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E.
如图所示,已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点C的坐标为(8,4),将△ABC沿AB翻折,使C点落在该坐标平面内的D点处,AD交x轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
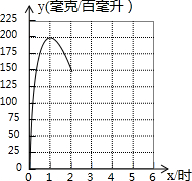 某医药研究所开发一种新药,实验数据显示,如果成人按规定的剂量服药,1.5小时内血液中含药量y1(毫克/百毫升)与时间x(时)的关系可以近似地用二次函数刻画(0≤x<1.5),服药后1小时,血液中含药量达到最高值200毫克/百毫升,1.5小时后(包含1.5小时),经过凋查,测得如下数据:
某医药研究所开发一种新药,实验数据显示,如果成人按规定的剂量服药,1.5小时内血液中含药量y1(毫克/百毫升)与时间x(时)的关系可以近似地用二次函数刻画(0≤x<1.5),服药后1小时,血液中含药量达到最高值200毫克/百毫升,1.5小时后(包含1.5小时),经过凋查,测得如下数据:| x | 1.5 | 2.5 | 3 | 4.5 | 5 | … |
| y | 150 | 90 | 75 | 50 | 45 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 该校所有初三学生是总体 | |
| B. | 所抽取的30名学生是样本 | |
| C. | 所抽取的15名学生是样本 | |
| D. | 所抽取的30名学生的体育成绩是样本 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -22=4 | B. | ${({-\frac{1}{2}})^{-2}}=4$ | C. | (-3)-1×3=1 | D. | (-1)2016=2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 5 | 3 | 1 | -1 | -3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛物线开口向上 | B. | 当x=1时,y的最大值为4 | ||
| C. | 对称轴直线是x=1 | D. | 抛物线与x轴的交点为(-1,0),(3,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com