
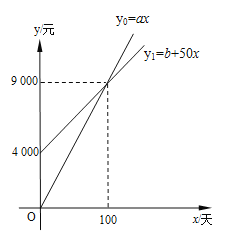
【题目】国家推行“节能减排,低碳经济”政策后,某企业推出一种“CNG”改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0,y1(元)与正常运营时间x(天)之间分别满足关系式:y0=ax,y1=b+50x,图象如图所示.
(1)每辆车改装前每天的燃料费a= 元,每辆车的改装费b= 元,正常运营时间 天后,就可以从节省的燃料费中收回改装成本;
(2)某出租汽车公司一次性改装了100辆出租车,因而正常运行多少天后共节省燃料费40万元?
【答案】(1)90,4000,100;(2)200.
【解析】试题分析:(1)根据图象得出y0=ax过点(100,9000),得出a的值,再将点(100,9000),代入y1=b+50x,求出b即可,再结合图象得出正常营运100天后从节省的燃料费中收回改装成本;
(2)根据题意及图象得出:改装前、后的燃料费燃料费每天分别为90元,50元,进而得出100×(90﹣50)x=400000+100×4000,得出即可
试题解析:解:(1)∵y0=ax过点(100,9000),得出a=90,将点(100,9000),代入y1=b+50x,b=4000,根据图象得出正常营运100天后从节省的燃料费中收回改装成本.
故答案为:a=90;b=4000,100;
(2)依据题意及图象得:改装前、后的燃料费燃料费每天分别为90元,50元,则:100×(90﹣50)x=400000+100×4000,解得:x=200.
答:200天后共节省燃料费40万元.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;
x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;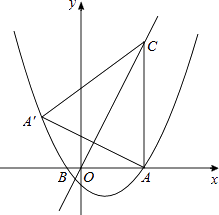
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx经过A(4,0),B(1,3)两点,点B、C关于抛物线的对称轴l对称,过点B作直线BH⊥x轴,交x轴于点H.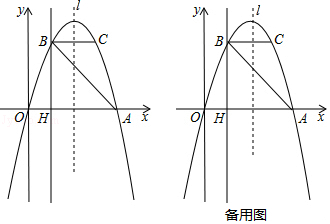
(1)求抛物线的解析式;
(2)若点M在直线BH上运动,点N在x轴上运动,是否存在这样的点M、N,使得以点M为直角顶点的△CNM是等腰直角三角形?若存在,请求出点M、N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(![]() )×(﹣36)
)×(﹣36)
(2)﹣32+(﹣![]() )2×(﹣
)2×(﹣![]() )+|﹣22|+(﹣1)2013;
)+|﹣22|+(﹣1)2013;
(3)36×(﹣99![]() );
);
(4)﹣13×![]() ﹣0.34×
﹣0.34×![]() +
+![]() ×(﹣13)﹣
×(﹣13)﹣![]() ×0.34(用简便方法计算)
×0.34(用简便方法计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1(注:与图2完全相同),二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.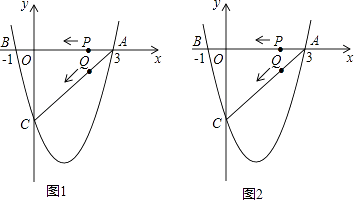
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )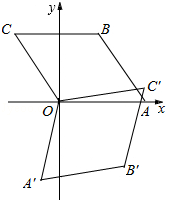
A.( ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(2,﹣2)
D.( ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
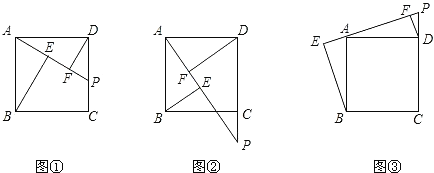
【题目】在正方形ABCD中,点P是CD边上一动点,连接PA,分别过点B、D作![]() 、
、![]() ,垂足分别为E、F.
,垂足分别为E、F.
![]() 如图
如图![]() ,请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?
,请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?
![]() 若点P在DC的延长线上,如图
若点P在DC的延长线上,如图![]() ,那么这三条线段的长度之间又具有怎样的数量关系?
,那么这三条线段的长度之间又具有怎样的数量关系?
![]() 若点P在CD的延长线上,如图
若点P在CD的延长线上,如图![]() ,请直接写出结论.
,请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,将菱形沿EF折叠,点B正好落在AD边的点G处,且EG⊥AC,若CD=8,则FG的长为( ) 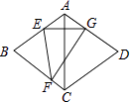
A.4 ![]()
B.4 ![]()
C.4 ![]()
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com