
分析 (1)要证明方程总有两个不相等的实数根,那么只要证明△>0即可;
(2)要使方程有整数解,那么$\frac{5±\sqrt{9+4p}}{2}$为整数即可,于是p可取0,4,10时,方程有整数解.
解答 解:(1)原方程可化为x2-5x+4-p2=0,
∵△=(-5)2-4×(4-p2)=4p2+9>0,
∴不论p为任何实数,方程总有两个不相等的实数根;
$\frac{5±\sqrt{9+4{p}^{2}}}{2}$,
(2)原方程可化为x2-5x+4-p2=0,
∵方程有整数解,
∴$\frac{5±\sqrt{9+4{p}^{2}}}{2}$为整数即可,
∴p可取0,2,-2时,方程有整数解.
点评 本题考查了一元二次方程的根的情况,判别式△的符号,把求未知系数的范围的问题转化为解不等式的问题是解题的关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 11.4×102 | B. | 1.14×103 | C. | 1.14×104 | D. | 1.14×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
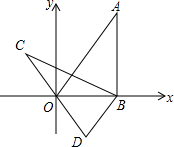 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( )| A. | (-1,$\sqrt{3}$) | B. | (-2,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (-$\sqrt{3}$,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 生活费(元) | 10 | 15 | 20 | 25 | 30 |
| 学生人数(人) | 4 | 10 | 15 | 10 | 6 |
| A. | 平均数是20 | B. | 众数是20 | C. | 中位数是20 | D. | 极差是20 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
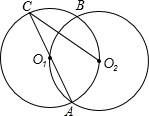 如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1,并延长交⊙O1于点C,则∠ACO2的度数为( )
如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1,并延长交⊙O1于点C,则∠ACO2的度数为( )| A. | 60° | B. | 45° | C. | 30° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E为正方形ABCD边延长线上一点,AE交CD于F点,FG∥AD交DE于G点,其中有△ABE∽△FCE,△EFG∽△EAD,请探求CF与FG的大小关系,并说明理由.
如图,点E为正方形ABCD边延长线上一点,AE交CD于F点,FG∥AD交DE于G点,其中有△ABE∽△FCE,△EFG∽△EAD,请探求CF与FG的大小关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com