Question

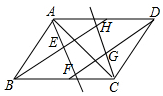
3．如图，已知?ABCD的四个内角的平分线分别相交于点E、F、G、H，连接AC．若EF=2，FG=GC=5，则AC的长是（　　）

• A． 12
• B． 13
• C． $6\sqrt{5}$
• D． $8\sqrt{3}$

Answer 1

分析 如图，设AC与DF交于M，AC与EH交于N．易证四边形EFGH是矩形，△ABE≌△CDG，△AEN≌△CGM，推出FG=EH=CG=5，EF=GH=2，CH=7，EN=GM，CM=AN，由EH=FG，推出FM=NH，设GM=EN=x，则HN=FN=5-x，由GM∥HN，可得$\frac{MG}{HN}$=$\frac{CG}{CH}$，可得$\frac{x}{5-x}$=$\frac{5}{7}$，推出x=$\frac{25}{12}$，在Rt△CMG中，可得CM=AN=$\sqrt{{5}^{2}+（\frac{25}{12}）^{2}}$=$\frac{65}{12}$，在Rt△CNH中，求出CN即可解决问题．

解答 解：如图，设AC与DF交于M，AC与EH交于N．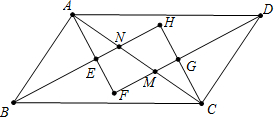

∵四边形ABCD是平行四边形，?ABCD的四个内角的平分线分别相交于点E、F、G、H，
∴易证四边形EFGH是矩形，△ABE≌△CDG，△AEN≌△CGM，
∴FG=EH=CG=5，EF=GH=2，CH=7，EN=GM，CM=AN，
∵EH=FG，
∴FM=NH，设GM=EN=x，则HN=FN=5-x，
∵GM∥HN，
∴$\frac{MG}{HN}$=$\frac{CG}{CH}$，
∴$\frac{x}{5-x}$=$\frac{5}{7}$，
∴x=$\frac{25}{12}$，
在Rt△CMG中，CM=AN=$\sqrt{{5}^{2}+（\frac{25}{12}）^{2}}$=$\frac{65}{12}$，
在Rt△CNH中，CN=$\sqrt{{7}^{2}+（\frac{35}{12}）^{2}}$=$\frac{91}{12}$，
∴AC=AN+CN=$\frac{65}{12}$+$\frac{91}{12}$=13，
故选B．

点评 本题考查平行四边形的性质、矩形的判定和性质、全等三角形的判定和性质、勾股定理、平行线分线段成比例定理等知识，本题的综合性比较强，解题的关键是灵活运用所学知识解决问题，学会利用参数，构建方程解决问题，属于中考选择题中的压轴题．