
 如图,△ABC的周长为18cm,BE、CF分别为AC、AB边的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,S△ABC=36cm2.
如图,△ABC的周长为18cm,BE、CF分别为AC、AB边的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,S△ABC=36cm2.分析 (1)根据中线的概念求出AB、AC的长,根据周长公式求出BC,根据重心的概念得到AD是BC边上的中线,得到答案;
(2)根据三角形的中线把三角形分为面积相等的两部分和重心的性质计算即可.
解答 解:(1)BE、CF分别为AC、AB边的中线,
∴AB=2AF=6cm,AC=2AE=4cm,又△ABC的周长为18cm,
∴BC=8cm,
∵中线BE、CF相交于点O,
∴点O是三角形的重心,
∴AD是BC边上的中线,
∴BD=$\frac{1}{2}$CB=4cm;
(2)∵AD是BC边上的中线,S△ABC=36cm2,
∴S△ABD=18cm2.
∵点O是三角形的重心,
∴AO=2OD,
∴S△BOD=6cm2.
点评 本题考查的是三角形的重心和三角形的面积的计算,掌握三角形的重心是三角形三条中线的交点、三角形的中线把三角形分为面积相等的两部分是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
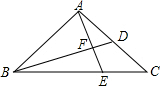 如图,在△ABC中,BD为AC边上的中线,BE=AB,且AE与BD相交于点F,求证:$\frac{AB}{BC}$=$\frac{EF}{AF}$.
如图,在△ABC中,BD为AC边上的中线,BE=AB,且AE与BD相交于点F,求证:$\frac{AB}{BC}$=$\frac{EF}{AF}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
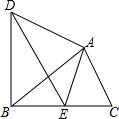 如图,△ABC绕点A顺时针旋转得△ADE,点E恰好落在边BC上.
如图,△ABC绕点A顺时针旋转得△ADE,点E恰好落在边BC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com