
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
【答案】
(1)证明:如图,连接AC
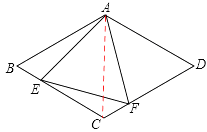
∵四边形ABCD为菱形,∠BAD=120°,
∠BAE+∠EAC=60°,∠FAC+∠EAC=60°,
∴∠BAE=∠FAC
∵∠BAD=120°,
∴∠ABC=60°.
∴△ABC和△ACD为等边三角形
∴∠ACF=60°,AC=AB
∴∠ABE=∠ACF
∴在△ABE和△ACF中,
∵∠BAE=∠FAC,AB=AC,∠ABE=∠ACF,
∴△ABE≌△ACF(ASA)
∴BE=CF
(2)解:四边形AECF的面积不变,△CEF的周长发生变化.理由如下:
由(1)得△ABE≌△ACF,则 ![]() .
.
∴ ![]() ,是定值
,是定值
作AH⊥BC于H点,则BH=2,
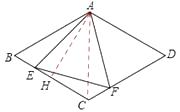
![]() .
.
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE
由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小=4+ ![]() ,
,
【解析】 (1)连接AC,根据菱形的对角线平分一组对角知:∠BAE+∠EAC=60°,∠FAC+∠EAC=60°,从而得出∠BAE=∠FAC,根据菱形四边相等及对角相等得出△ABC和△ACD为等边三角形,根据等边三角形的性质得出∠ACF=60°,AC=AB,然后由ASA判断出△ABE≌△ACF,根据全等三角形对应边相等得出BE=CF;
(2)四边形AECF的面积不变,△CEF的周长发生变化.理由如下:根据全等三角形的面积相等得出 S Δ A B E = S Δ A C F ,故S 四 边 形 A E C F = S Δ A E C + S Δ A C F = S Δ A E C + S Δ A B E = S Δ A B C ,是定值;作AH⊥BC于H点,则BH=2,![]() △CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE,由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小。
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE,由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小。
【考点精析】本题主要考查了垂线段最短和菱形的性质的相关知识点,需要掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,3).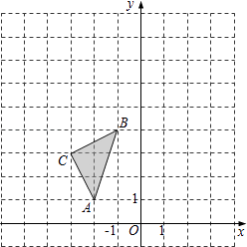
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出A1点的坐标及sin∠B1A1C1的值;
以原点O为位似中心,位似比为1:2,在y轴的左侧,画出 将△ABC放大后的△A2B2C2 , 并写出A2点的坐标;
(2)若点D(a,b)在线段AB上,直接写出经过(2)的变化后点D的对应点D2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.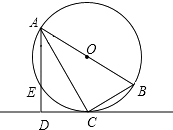
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2 ![]() cm,求弦AE的长.
cm,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知两直线,L1:y=k1x+b1,L2:y=k2x+b2,
若L1⊥L2,则有k1k2=﹣1,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx﹣1垂直,求k的值;
(2)若一条直线经过A(2,3),且与y=﹣![]() x+3垂直,求这条直线所对应的一次函数的关系式.
x+3垂直,求这条直线所对应的一次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,∠ABC=90°.以AB为斜边作等腰直角三角形ADB.点P是直线DB上一个动点,连接AP,作PE⊥AP交BC所在的直线于点E.

(1)如图1,点P在BD的延长线上,PE⊥EC,AD=1,直接写出PE的长;
(2)点P在线段BD上(不与B,D重合),依题意,将图2补全,求证:PA=PE;
(3)点P在DB的延长线上,依题意,将图3补全,并判断PA=PE是否仍然成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开设篮球、足球、乒乓球、排球四个项目的选修课,为了解同学们的报名情况,随机抽取了部分学生进行调査,将获得的数据进行整理,绘制了如下两幅不完整的统计图,请你根据统计图提供的信息,完成下列问题:

(1)把条形统计图1补充完整,写出图2中C所在扇形的圆心角是 °;
(2)若该校有3000名学生,请你估计全校大约有多少名学生会选修足球课.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简求值
(1)6x+7x2﹣9+4x﹣x2+6
(2)5m﹣2(4m+5n)+3(3m﹣4n)
(3)先化简,再求值:5(3a2b﹣ab2)﹣(ab2+3a2b),其中a=﹣![]() ,b=
,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋子中装有大小完全相同的3粒乒乓球,其中2粒白色,1粒黄色.请你用它为甲、乙两位同学设计一个能决定胜负的公平的摸球游戏规则.并说明公平的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com