
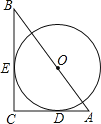
【题目】如图,⊙O的圆心在Rt△ABC的斜边AB上,且⊙O分别与边AC、BC相切于D、E两点,已知AC=3,BC=4,则⊙O的半径r=_____.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
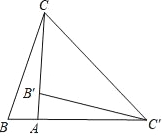
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对70周年国庆阅兵仪式直播的收看情况,某校对部分学生进行了一次调査,调査直播收看情况分三种:A.全程收看直播;B.观看了一部分直播;C.没有观看.学校学生会将调査数据进行了整理,并绘制了如下两幅不完整的统计图,请根据相关信息,解答下列问题:
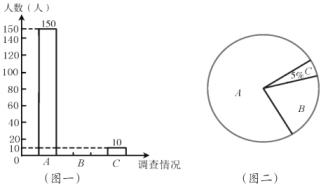
(1)本次活动共调查了______名学生;
(2)图二中![]() 区域的圆心角的度数为______;
区域的圆心角的度数为______;
(3)补全图;
(4)若该校学生共有3000名,请估计该校学生全程收看直播的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
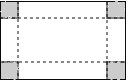
【题目】如图,有一块矩形硬纸板,长50cm,宽30cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为600cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】街道旁边有一根电线杆AB和一块半圆形广告牌,有一天,小明突然发现,在太阳光照射下,电线杆的顶端A的影子刚好落在半圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在地面上一点E,已知BC=5米,半圆形的直径为6米,DE=2米.求电线杆的高度.
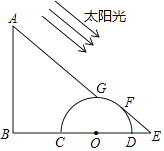
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=CB,D是边AC的中点,过点D做DE⊥BC于E.
(1)以边AB为直径作⊙O,作图要求:尺规作图,保留作图痕迹,不写作法;
(2)在(1)条件下,判断DE与圆O是否相切?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】非洲猪瘟疫情发生以来,猪肉市场供应阶段性偏紧和猪价大幅波动时有发生,为稳定生猪生产,促进转型升级,增强猪肉供应保障能力,国务院办公厅于2019年9月印发了《关于稳定生猪生产促进转型升级的意见》,某生猪饲养场积极响应国家号召,努力提高生产经营管理水平,稳步扩大养殖规模,增加猪肉供应量。该饲养场2019年每月生猪产量y(吨)与月份x(![]() ,且x为整数)之间的函数关系如图所示.
,且x为整数)之间的函数关系如图所示.
(1)请直接写出当![]() (x为整数)和
(x为整数)和![]() (x为整数)时,y与x的函数关系式;
(x为整数)时,y与x的函数关系式;
(2)若该饲养场生猪利润P(万元/吨)与月份x(![]() ,且x为整数)满足关系式:
,且x为整数)满足关系式:![]() ,请问:该饲养场哪个月的利润最大?最大利润是多少?
,请问:该饲养场哪个月的利润最大?最大利润是多少?
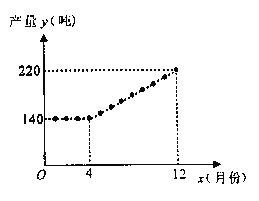
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com