��֪����ƽ��ֱ������ϵxOy�У����κ���y=-x2+bx+c��ͼ����x�ύ��A��B���㣬��A�ڵ�B����ֱ࣬��y=kx+3��ö��κ�����ͼ����D��B���㣬���е�D��y���ϣ���B������Ϊ��3��0����
��1����k��ֵ��������κ����Ľ���ʽ��
��2���������ߵĶ���ΪC����FΪ�߶�DB��һ�㣬��ʹ�á�DCF=��ODB�������ʱ��F�����꣮
��3���ڣ�2���������£�����PΪֱ��DB�ϵ�һ�����㣬����P��x��Ĵ�����������κ�����ͼ���ڵ�E���ʣ��Ƿ���������ĵ�P��ʹ���Ե�P��C��E��FΪ������ı�����ƽ���ı��Σ������ڣ������P�ĺ����ꣻ�������ڣ���˵�����ɣ�
��������1���������ȸ���ֱ��y=kx+3�͵�B��������뼴�����k��ֵ�����е�D�����������κ���y=-x2+bx+c�У��������b��c��ֵ����������𰸣�
��2���������ȸ���ͼ�εó���C�����꣬�ٸ�����֪�����ij���ODB�Ķ�������������D���������߶Գ���Ĵ��ߣ��Ӷ��ó���F�����꣮
��3�����������жϳ����������ĵ㣬�ٸ�����֪�����ó��Ե�P��C��E��FΪ������ı�����ƽ���ı��Σ��������P�͵�E�����꣬�Ӷ��ó�x��ֵ�����������P�ĺ����꣮
���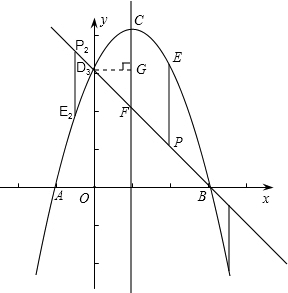
�⣺��1����ֱ��y=kx+3������B��3��0����
������k=-1��
�������֪����D������Ϊ��0��3����
��������y=-x
2+bx+c������B�͵�D��
���
�������ߵĽ���ʽΪ
y=-x
2+2x+3��
��2����ͼ������C������Ϊ��1��4����
�����⣬��֪��ODB=45�㣮
����D���������߶Գ���Ĵ���DG��
��֪DG=CG=1��
���Դ�ʱ��DCG=45�㣬
����֪��F������Ϊ��1��2����
��3�����������ĵ�P��ʹ���Ե�P��C��E��FΪ������ı�����ƽ���ı��Σ�
�������£�������֪PE��CF��
��Ҫʹ�Ե�P��C��E��FΪ������ı�����ƽ���ı��Σ�ֻҪ����PE=CF=2���ɣ�
�ߵ�P��ֱ��DB�ϣ�
������P��������x��-x+3����
�ߵ�E��������y=-x
2+2x+3�ϣ�
������E��������x��-x
2+2x+3����
�൱-x+3-��-x
2+2x+3��=2ʱ�����
x=��
��-x
2+2x+3-��-x+3��=2ʱ�����x=1��x=2��
x=1�������⣬��ȥ��
����������ĵ�P�ĺ�����ֱ�Ϊ
x1=��
x2=��x
3=2��
������������Ҫ�����˶��κ�������ʽ��ȷ������������֪ʶ�㣮��Ҫ����ѧ�����ν�ϵ���ѧ˼�뷽����

 �⣺��1����ֱ��y=kx+3������B��3��0����
�⣺��1����ֱ��y=kx+3������B��3��0����

 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�

 ��ͼ����ƽ��ֱ�������У���ֱ֪��y=kx+b��ֱ��y=
��ͼ����ƽ��ֱ�������У���ֱ֪��y=kx+b��ֱ��y= ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=