
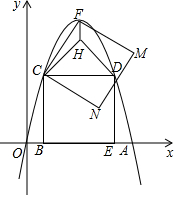
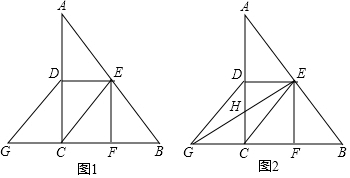
 如图,在平面直角坐标系中,抛物线y=ax2-6ax(a<0)与x轴正半轴交于点A,矩形BCDE的顶点B、E均在x轴上,C、D均在抛物线上,且点B的坐标为(1,0),抛物线的顶点为F,以CF为边作正方形CFMN,以CD为底边向上作等腰直角三角形CDH,连结FH.
如图,在平面直角坐标系中,抛物线y=ax2-6ax(a<0)与x轴正半轴交于点A,矩形BCDE的顶点B、E均在x轴上,C、D均在抛物线上,且点B的坐标为(1,0),抛物线的顶点为F,以CF为边作正方形CFMN,以CD为底边向上作等腰直角三角形CDH,连结FH.分析 (1)先求得抛物线的对称轴方程为x=3,然后求得C(1,-5a),F(3,-9a),依据等腰直角三角形的性质求得△CDH的CD边上的高为2,则可表示出EH的长;
(2)先求得△CDF的CD边上的高为2$\sqrt{3}$,然后依据Fy-Cy=2$\sqrt{3}$列方程求解即可;
(3)当点N落在对称轴上时,点H与点F重合,即FH=-4a-2=0;
(4)首先根据题意画出符合题意的图形,然后找出图中全等的三角形,然后依据全等三角形的性质求得相关线段的长,然后列出关于a的方程求解即可.
解答 解:(1)抛物线的对称轴为x=$\frac{6a}{2a}$=3,
由题意可知点C与点D关于x=3对称,
∴CD=4.
当x=1,y=a-6a=-5a,
∴C(1,-5a).
∵CDH为等腰直角三角形,CD=4,
∴CD边上的高=2.
当x=3时,y=9a-18a=-9a.
∴FH=-9a-(-5a+2)=-4a-2.
(2)当△FCD为等边三角形时,△CDF的CD边上的高=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
∴-4a-2+2=2$\sqrt{3}$,解得:a=-$\frac{\sqrt{3}}{2}$.
(3)当点N落在对称轴上时,点H与点F重合,即FH=-4a-2=0,
解得:a=-$\frac{1}{2}$.
∴抛物线的解析式为y=-$\frac{1}{2}$x2+3x.
(4)如图1所示: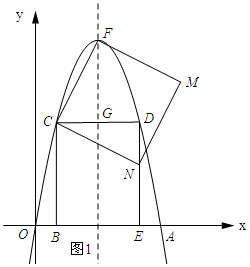
∵∠DCN+∠CND=90°,∠DCN+∠FCG=90°.
∴∠CND=∠FCG.
在△CGF和△NDC中$\left\{\begin{array}{l}{∠CND=∠FCG}\\{∠NDC=∠CGF}\\{CF=CN}\end{array}\right.$,
∴△CGF≌△NDC.
∴CD=FG=4.
∵GF=-9a-(-5a)=-4a,
∴-4a=4,解得a=-1.
如图2所示:当点M与点D重合时,点N在抛物线的对称轴上.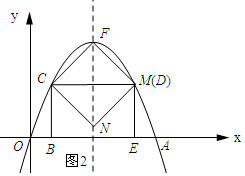
由(3)可知a=-$\frac{1}{2}$.
如图3所示:当点N在BE上时.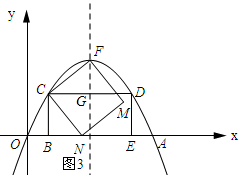
∵∠BCN+∠NCG=90°,∠NCG+∠GCF=90°,
∴∠BCN=∠GCF.
在△BCN和△GCF中$\left\{\begin{array}{l}{∠BCN=∠GCF}\\{∠CBN=∠CGF}\\{CN=CF}\end{array}\right.$,
∴△BCN≌△GCF.
∴BC=CG=2,即-5a=2,解得:a=-$\frac{2}{5}$.
如图4所示: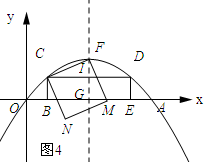
∵∠CFI+∠MFG=90°,∠MFG+∠FGM=90°,
∴∠CFI=∠FMG.
在△CFI和△FMG中$\left\{\begin{array}{l}{∠CFI=∠FMG}\\{∠FIC=∠FGM=90°}\\{CF=FM}\end{array}\right.$,
∴△CFI≌△FMG.
∴FG=CI=2,即-9a=2,解得:a=-$\frac{2}{9}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数的对称性,等腰直角三角形的性质,等边三角形的性质、正方形的性质以及全等三角形的性质和判定,依据题意画出符合题意的图形是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC
如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC查看答案和解析>>
科目:初中数学 来源: 题型:选择题
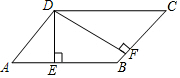 如图,若?ABCD的周长为36cm,过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,?ABCD的面积为( )cm.
如图,若?ABCD的周长为36cm,过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,?ABCD的面积为( )cm.| A. | 40 | B. | 32 | C. | 36 | D. | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
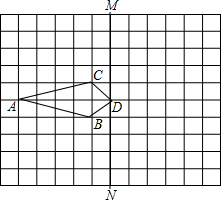 如图,四边形ABDC的四个顶点都在正方形网格中的小正方形顶点上,每个小正方形的边长为1.
如图,四边形ABDC的四个顶点都在正方形网格中的小正方形顶点上,每个小正方形的边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
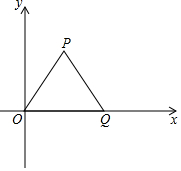 如图△OPQ是边长为$\sqrt{2}$的等边三角形,若反比例函数y=$\frac{k}{x}$的图象过点P.
如图△OPQ是边长为$\sqrt{2}$的等边三角形,若反比例函数y=$\frac{k}{x}$的图象过点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com