解:(1)AB=CD+BD,
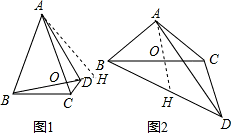
证明:延长BD至H,使BH=AB,
∵∠ABD=60°,
∴△ABH为等边三角形,
∴∠H=60°,AH=AB,
∵AB=AC,
∴∠ABC=∠ACB,AC=AH,
∵∠ADB=∠ACB,∠ABC=∠ADB,
又∵∠AOB=∠CAD+∠ADB=∠CBD+∠ACB,
∴∠CBD=∠CAD,
∵∠ABC=∠ABD+∠CBD=60°+∠CBD,
又∵∠ADB=∠H+∠HAD=60°+∠HAD
∴∠CBD=∠HAD
∴∠CAD=∠HAD,
在△ACD和△AHD中
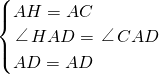
∴△ACD≌△AHD,
∴DC=DH,
∴AB=CD+BD.
(2)解:不成立,AB=BD-CD,
理由是:在BD上取一点H,使BH=AB,
同理可证∠CBD=∠CAD=60°-∠ABC,∠DAH=60°-∠ADB,
同理可证△ACD≌△AHD,
∴DC=DH,
即AB=BD-CD.
分析:(1)延长BD至H,使BH=AB,得出△ABH为等边三角形,推出∠H=60°,AH=AB,根据等腰三角形的性质推出∠CBD=∠CAD,根据三角形的外角性质推出∠CAD=∠HAD,证△ACD≌△AHD,推出DC=DH即可;
(2)不成立,AB=BD-CD,在BD上取一点H,使BH=AB,与(1)类似证出∠CBD=∠CAD=60°-∠ABC,∠DAH=60°-∠ADB,△ACD≌△AHD,推出DC=DH即可.
点评:本题考查了等腰三角形的性质,三角形的外角性质,全等三角形的性质和判定,等边三角形的性质和判定等知识点的应用,关键是正确作辅助线(证三条线段之间的关系的解题思路),题目比较典型,有一点难度.

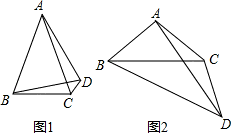 如图1,等腰△ABC,AB=AC,∠A<60°,D为△ABC外部一点,在AB的右侧作∠ABD=60°,且∠ADB=∠ACB
如图1,等腰△ABC,AB=AC,∠A<60°,D为△ABC外部一点,在AB的右侧作∠ABD=60°,且∠ADB=∠ACB


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案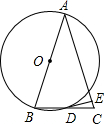 结论是否成立?请说明理由;
结论是否成立?请说明理由;