
【题目】已知直线l及直线l外一点P.如图,
(1)在直线l上取一点A,连接PA;
(2)作PA的垂直平分线MN,分别交直线l,PA于点B,O;
(3)以O为圆心,OB长为半径画弧,交直线MN于另一点Q;
(4)作直线PQ.
根据以上作图过程及所作图形,下列结论中错误的是( )
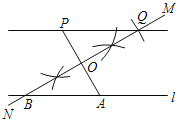
A.△OPQ≌△OABB.PQ∥AB
C.AP=![]() BQD.若PQ=PA,则∠APQ=60°
BQD.若PQ=PA,则∠APQ=60°
【答案】C
【解析】
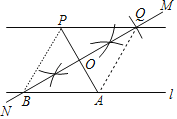
连接AQ,BP,如图,利用基本作图得到BQ垂直平分PA,OB=OQ,则可根据“SAS”判断△OAB≌△OPQ,根据全等三角形的性质得∠ABO=∠PQO,于是可判断PQ∥AB;由BQ垂直平分PA得到QP=QA,若PQ=PA,则可判断△PAQ为等边三角形,于是得到∠APQ=60°,从而可对各选项进行判断.
解:连接AQ,BP,如图,
由作法得BQ垂直平分PA,OB=OQ,
∴∠POQ=∠AOB=90°,OP=OA,
∴△OAB≌△OPQ(SAS);
∴∠ABO=∠PQO,
∴PQ∥AB;
∵BQ垂直平分PA,
∴QP=QA,
若PQ=PA,则PQ=QA=PA,此时△PAQ为等边三角形,则∠APQ=60°.
故选:C.


科目:初中数学 来源: 题型:
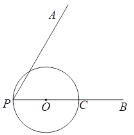
【题目】如图,∠APB,点C在射线PB上,PC为⊙O的直径,在∠APB内部且到∠APB两边距离都相等的所有的点组成图形M,图形M交⊙O于D,过点D作直线DE⊥PA,分别交射线PA,PB于E,F.
(1)根据题意补全图形;
(2)求证:DE是⊙O的切线;
(3)如果PC=2CF,且![]() ,求PE的长.
,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD为矩形,曲线L经过点D.点Q是四边形ABCD内一定点,点P是线段AB上一动点,作PM⊥AB交曲线L于点M,连接QM.
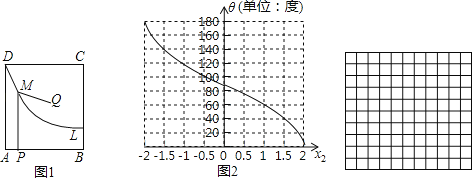
小东同学发现:在点P由A运动到B的过程中,对于x1=AP的每一个确定的值,θ=∠QMP都有唯一确定的值与其对应,x1与θ的对应关系如表所示:
x1=AP | 0 | 1 | 2 | 3 | 4 | 5 |
θ=∠QMP | α | 85° | 130° | 180° | 145° | 130° |
小芸同学在读书时,发现了另外一个函数:对于自变量x2在﹣2≤x2≤2范围内的每一个值,都有唯一确定的角度θ与之对应,x2与θ的对应关系如图2所示:
根据以上材料,回答问题:
(1)表格中α的值为 .
(2)如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等,可以在两个变量x1与x2之间建立函数关系.
①在这个函数关系中,自变量是 ,因变量是 ;(分别填入x1和x2)
②请在网格中建立平面直角坐标系,并画出这个函数的图象;
③根据画出的函数图象,当AP=3.5时,x2的值约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
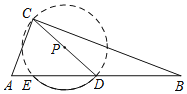
【题目】在△ABC中,以AB边上的中线CD为直径作圆,如果与边AB有交点E(不与点D重合),那么称![]() 为△ABC的C﹣中线弧.例如,如图中
为△ABC的C﹣中线弧.例如,如图中![]() 是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
(1)当t=2时,
①在点C1(﹣3,2),C2(0,2![]() ),C3(2,4),C4(4,2)中,满足条件的点C是 ;
),C3(2,4),C4(4,2)中,满足条件的点C是 ;
②若在直线y=kx(k>0)上存在点P是△ABC的C﹣中线弧![]() 所在圆的圆心,其中CD=4,求k的取值范围;
所在圆的圆心,其中CD=4,求k的取值范围;
(2)若△ABC的C﹣中线弧![]() 所在圆的圆心为定点P(2,2),直接写出t的取值范围.
所在圆的圆心为定点P(2,2),直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线x=5与直线y=3,x轴分别交于点A,B,直线y=kx+b(k≠0)经过点A且与x轴交于点C(9,0).
(1)求直线y=kx+b的表达式;
(2)横、纵坐标都是整数的点叫做整点.记线段AB,BC,CA围成的区域(不含边界)为W.
①结合函数图象,直接写出区域W内的整点个数;
②将直线y=kx+b向下平移n个单位,当平移后的直线与区域W没有公共点时,请结合图象直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,AB,CD,EF,GH是正方形OPQR边上的线段,点M在其中某条线段上,若射线OM与x轴正半轴的夹角为α,且sinα>cosα,则点M所在的线段可以是( )
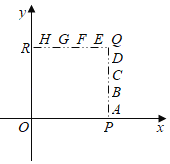
A.AB和CDB.AB和EFC.CD和GHD.EF和GH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张完全相同的卡片的正面分别画有等边三角形、平行四边形、矩形、菱形、正方形,将其背面朝上放在桌面上,从中随机抽取一张,所抽取的卡片上的图形既是轴对称图形,又是中心对称图形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
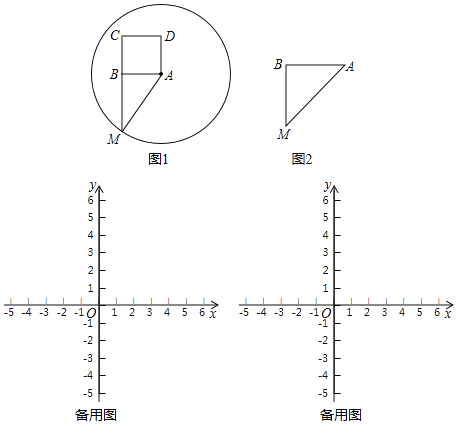
【题目】在△ABM中,∠ABM=90°,以AB为一边向△ABM的异侧作正方形ABCD,以A为圆心,AM为半径作⊙A,我们称正方形ABCD为⊙A的“关于△ABM的友好正方形”,如果正方形ABCD恰好落在⊙A的内部(或圆上),我们称正方形ABCD为⊙A的“关于△ABM的绝对友好正方形”,例如,图1中正方形ABCD是⊙A的“关于△ABM的友好正方形”.
(1)图2中,△ABM中,BA=BM,∠ABM=90°,在图中画出⊙A的“关于△ABM的友好正方形ABCD”.
(2)若点A在反比例函数y=![]() (k>0,x>0)上,它的横坐标是2,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求k的取值范围.
(k>0,x>0)上,它的横坐标是2,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求k的取值范围.
(3)若点A是直线y=﹣x+2上的一个动点,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求出点A的横坐标m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com