
【题目】如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.

【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)由D是BC中点,得到BD=CD,通过AAS证明△BED≌△CFD,得到ED=FD,再由对角线互相平分的四边形是平行四边形即可得到结论;
(2)与△ABD面积相等的三角形有△ACD、△CEF、△BEF、△BEC、△BFC.
试题解析:(1)证明:∵D是BC中点,∴BD=CD.
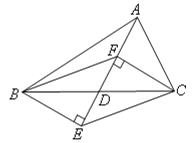
∵BE⊥AE,CF⊥AE,∴∠BED=∠CFD=900.在△BED与△CFD中,∵∠BED=∠CFD,∠BDE=∠CDF,BD=CD,∴△BED≌△CFD(AAS),∴ED=FD .∵BD=CD,∴四边形BFEC是平行四边形.
(2)与△ABD面积相等的三角形有△ACD、△CEF、△BEF、△BEC、△BFC.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
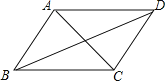
A. AB//CD, AD=BCB. ∠B=∠C,∠A=∠D
C. AB=AD, BC=CDD. AB=CD, AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=![]() (k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=
(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
(1)求反比例函数的表达式.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
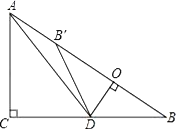
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
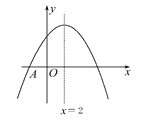
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-2,0),顶点坐标为(2,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①当x>6时,y<0;②5a+b>0;③![]() ≤a≤-
≤a≤-![]() ,④4≤n<5中,正确有( )
,④4≤n<5中,正确有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,初中学生课桌椅不合格率达76.7%(不合格是指不能按照学生不同的身高来调节课桌椅的高度),为了解初中生的身高情况,随机抽取了某校初中部分男生、女生进行调查收集数据如下:
男生身高(单位:cm):163 161 160 163 161 162 163 164 163 163
女生身高(单位:cm):164 161 160 161 161 162 160 162 163 162
整理数据:
160 | 161 | 162 | 163 | 164 | |
男生(人) | 1 | 2 | 1 | a | 1 |
女生(人) | 2 | b | 3 | 1 | 1 |
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)现有两名身高都为163cm的男生和女生,比较这两名同学分别在男生、女生中的身高情况,并简述理由;
(3)根据相关研究发现,只有身高为161cm的初中生课桌椅是合格的,试估计全校1000名学生中,有多少名学生的课桌椅是合格的?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣![]() x2+
x2+![]() x+4经过A、B两点.
x+4经过A、B两点.

(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,是否存在t,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某学校高中两个班的学生上学时步行、骑车、乘公交、乘私家车人数的扇形统计图,已知乘公交人数是乘私家车人数的2倍.若步行人数是18人,则下列结论正确的是( )

A. 被调查的学生人数为90人
B. 乘私家车的学生人数为9人
C. 乘公交车的学生人数为20人
D. 骑车的学生人数为16人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com