
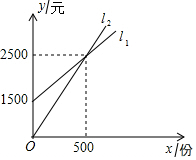
 某公司要印制产品宣传材料,l1反映了甲印刷厂的收费y1(元)与印制数量x(份)间的关系,l2反映了乙印刷厂的收费y2(元)与印制数量x(份)间的关系.
某公司要印制产品宣传材料,l1反映了甲印刷厂的收费y1(元)与印制数量x(份)间的关系,l2反映了乙印刷厂的收费y2(元)与印制数量x(份)间的关系.分析 (1)观察图象,即可判断.
(2)利用待定系数法即可解决问题.
(3)当y=4000时,分别求出自变量的取值即可判断.
解答 解:(1)由图象可知,当印制500份时,甲、乙印刷厂的收费相同.
(2)设l1的解析式为y=kx+b,
∵经过点(0,1500),(500,2500),
∴$\left\{\begin{array}{l}{b=1500}\\{500k+b=2500}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=1500}\end{array}\right.$,
∴l1的解析式为y=2x+1500,
设l2的解析式为y=k′x,则有500k′=2500,
∴k′=5,
∴l2的解析式为y=5x.
(3)由题意2x+1500=4000,x=1250,
5x=4000,x=800,
1250>800,
∴甲印刷厂印制的宣传材料份数较多.
点评 本题考查的是一次函数的应用问题,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出函数式,再求解.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
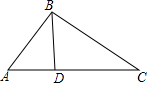 如图,在△ABC中,D是AC上一点,联结BD,∠CBD=∠A.
如图,在△ABC中,D是AC上一点,联结BD,∠CBD=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
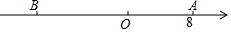 如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t<0)秒.
如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t<0)秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
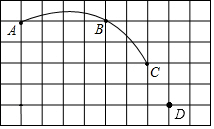 阅读下面的材料,回答问题:
阅读下面的材料,回答问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com