
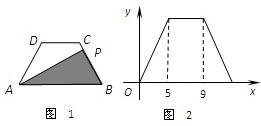
 11、如图1,在等腰梯形ABCD中,∠B=60°,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则梯形ABCD的周长是( )
11、如图1,在等腰梯形ABCD中,∠B=60°,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则梯形ABCD的周长是( )科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
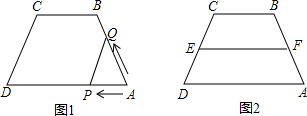 条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)
条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
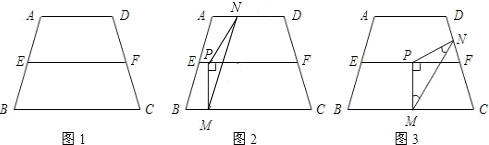
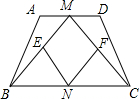 (2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题:
(2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:
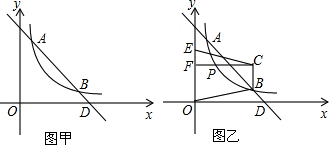
| k | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com