方程x2+2xy+3y2=34的整数解(x,y)的组数为( )
A.3
B.4
C.5
D.6
【答案】
分析:首先将原方程变形为:(x+y)
2+2y
2=34,即可得x+y必须是偶数,然后设x+y=2t,可得新方程2t
2+y
2=17,解此方程即可求得答案.
解答:解:方程变形得:(x+y)
2+2y
2=34,
∵34与2y
2是偶数,
∴x+y必须是偶数,
设x+y=2t,
则原方程变为:(2t)
2+2y
2=34,
∴2t
2+y
2=17,
它的整数解为
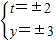
,
则当y=3,t=2时,x=1;
当y=3,t=-2时,x=-7;
当y=-3,t=2时,x=7;
当y=-3,t=-2时,x=-1.
∴原方程的整数解为:(1,3),(-7,3),(7,-3),(-1,-3)共4组.
故选B.
点评:此题考查了非一次不定方程的知识.此题难度较大,解题的关键是将原方程变形为:(x+y)
2+2y
2=34,由x+y必须是偶数,然后设x+y=2t,从而得新方程2t
2+y
2=17.

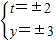 ,
,

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案