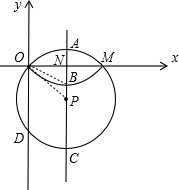
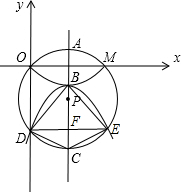
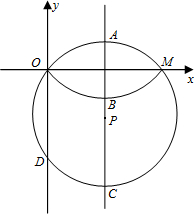
解:(1)连接OP,PM,设AC与OM交于N,
∵⊙P的半径为5,
∴AC=10,
∵点M(2m,0),
∴ON=MN=m,
∵点A到x轴的距离为h,
∴CN=AC-AN=10-h,
∴B(m,-h),C(m,h-10),
同理过P作OD的垂线,根据垂径定理即可得出OD=2PN=5-h,因此D点的坐标为(0,2h-10)
∴D(0,2h-10),
故答案为:(m,-h),(m,h-10),(0,2h-10);
(2)①设抛物线的解析式为y=a(x-4)
2-2,已知抛物线过D点,
因此-6=a(x-4)
2-2,
解得a=-

,
∴抛物线的函数关系式为:
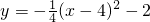
,
根据对称可知:E(8,-6);
②当m=4时,则C(4,-8),由①可知E的坐标为(8,-6),
设直线CE的解析式为y=kx+b,
则
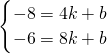
,
解得:
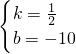
∴直线CE:
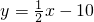
,
∴直线CE与y轴交于点R(0,-10),
当S
△CEQ=S
△CEP时,则QR=PC,
∴Q(0,-5)或Q(0,-15);
(3)假设以B、C、D、E为顶点的四边形组成菱形,则DE与BC互相垂直平分,设DE与BC相交于点F,于是BF=CF.
∴-h-2h+10=2h-10-h+10,即h=

,
∴AB=5
∴B、P两点重合,
∴
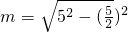
=


.:
分析:(1)可连接OP,PM,设AC与OM交于N,那么在直角三角形OPN中,ON=m,因此AN=BN=h,CN=AC-AN=10-h,所以B,C的坐标分别为(m,-h),(m,h-10),
同理过P作OD的垂线,根据垂径定理即可得出OD=2PN=5-h,因此D点的坐标为(0,2h-10);
(2)①可用顶点式二次函数通式来设抛物线的解析式,然后将D点的坐标代入即可求出抛物线的解析式.根据圆和抛物线的对称性可知:E点和D点关于抛物线的对称轴x=4对称,因此根据D的坐标即可求出E点的坐标.
②由①可知点E的坐标为(8,-6),所以可求出过CE的直线解析式,进而求出直线和x轴的交点坐标R,当S
△CEQ=S
△CEP则QR=PC,则可求出Q点坐标;
(3)如果以B、C、D、E为顶点的四边形组成菱形,那么这个四边形的对角线互相垂直平分,如果设BC,DE的交点为F,那么BF=CF,可用A点的纵坐标即AN的长表示出BF和CF由此可求出A点的纵坐标,进而可在直角三角形OAN中用勾股定理求出m的值.
点评:本题着重考查了待定系数法求二次函数解析式、一次函数的解析式、垂径定理、勾股定理、菱形的性质等重要知识点,综合性强,考查学生数形结合的数学思想方法.

 探索研究
探索研究
 ,
,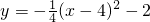 ,
,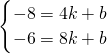 ,
,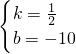
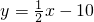 ,
,
 ,
,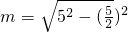 =
=
 .:
.:

 阅读快车系列答案
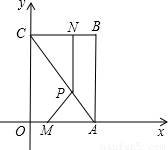
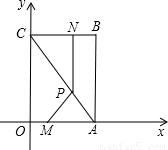
阅读快车系列答案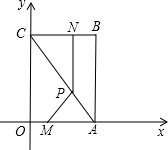 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒. 探索研究
探索研究