
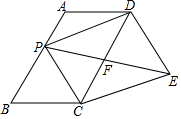
 在四边形ABCD中,AD∥BC,∠B=60°,AD=BC=4,AB=6,点P是直线AB上一动点.
在四边形ABCD中,AD∥BC,∠B=60°,AD=BC=4,AB=6,点P是直线AB上一动点.分析 (1)①根据一组对边平行且相等证明四边形ABCD是平行四边形,再由平行四边形的对角线互相平分可得结论;
②点C到直线AB的距离就是求CG的长,利用60度的三角函数计算即可;
(2)分两种情况:
①当P在线段AB上时,如图3,作辅助线,构建两平行线的距离CG和PH,利用△PDF∽△NCF,计算PF=$\frac{1}{4}×10\sqrt{3}$=$\frac{5\sqrt{3}}{2}$,CF=$\frac{3}{4}$×6=$\frac{9}{2}$,由勾股定理得:FH的长,最后求出AP的长;
②当P在BA的延长线上时,如图4,同理可得AP的长.
解答 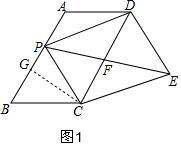 证明:(1)①∵AD∥BC,AD=BC,
证明:(1)①∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,
∴AB=CD,
∵四边形DPCE是平行四边形,
∴DF=CF=$\frac{1}{2}$CD,
∴DF=$\frac{1}{2}$AB;
②如图1,过C作CG⊥AB于G,则∠CGB=90°,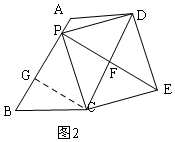
在Rt△CBG中,∵∠B=60°,BC=4,
∴sin∠B=$\frac{CG}{BC}$,即$\frac{CG}{4}=\frac{\sqrt{3}}{2}$,
∴CG=2$\sqrt{3}$,
∴点C到直线AB的距离是2$\sqrt{3}$;
③当PE⊥DC,且垂足F为DC的中点时,如图2,此时PE的长最小,
∴PE=2PF=2CG=4$\sqrt{3}$,
故答案为:4$\sqrt{3}$;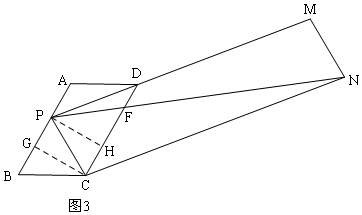
(2)分两种情况:
①当P在线段AB上时,如图3,过C作CG⊥AB于G,过P作PH⊥CD于H,
由(1)得:PH=CG=2$\sqrt{3}$,BG=2,
∵四边形PCNM是平行四边形,
∴PM∥CN,PM=CN,
∴△PDF∽△NCF,
∴$\frac{PD}{CN}=\frac{PF}{FN}$=$\frac{DF}{FC}$,
∵DM=2PD,
∴PM=3PD,
∴CN=3PD,
∴$\frac{PF}{FN}=\frac{1}{3}$=$\frac{DF}{FC}$,
∵PN=10$\sqrt{3}$,CD=6,
∴PF+FN=10$\sqrt{3}$,CF+DF=6,
∴PF=$\frac{1}{4}×10\sqrt{3}$=$\frac{5\sqrt{3}}{2}$,CF=$\frac{3}{4}$×6=$\frac{9}{2}$,
在Rt△PFH中,由勾股定理得:FH=$\sqrt{(\frac{5\sqrt{3}}{2})^{2}-(2\sqrt{3})^{2}}$=$\frac{3\sqrt{3}}{2}$,
∴CH=CF-FH=$\frac{9}{2}$-$\frac{3\sqrt{3}}{2}$,
∴PG=CH=$\frac{9}{2}$-$\frac{3\sqrt{3}}{2}$,
∴AP=AB-BG-PG=6-2-$\frac{9}{2}$+$\frac{3\sqrt{3}}{2}$=$\frac{3\sqrt{3}-1}{2}$;
②当P在BA的延长线上时,如图4,
过F作FH⊥AB于H,过C作CG⊥AB于G,
同理可知:FH=CG=2$\sqrt{3}$,BG=2,GH=CF=$\frac{9}{2}$,
PF=$\frac{5\sqrt{3}}{2}$,
由勾股定理得:PH=$\frac{3\sqrt{3}}{2}$,
∴AP=BG+GH+PH-AB=2+$\frac{9}{2}$+$\frac{3\sqrt{3}}{2}$-6=$\frac{3\sqrt{3}+1}{2}$;
综上所述,AP的长为$\frac{3\sqrt{3}-1}{2}$或$\frac{3\sqrt{3}+1}{2}$.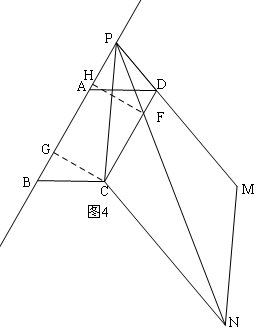
点评 本题是四边形的综合题,考查了平行四边形的性质、三角函数、点到直线的距离及垂线段最短,第2问有又难度,容易丢解,要注意最初条件:点P是直线AB上一动点,证明△PDF∽△NCF,并利用DM=2PD得出相似比为1:3是关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
| 行驶路程x(千米) | … | 100 | 150 | … |
| 油箱内剩余油量y(升) | … | 52 | 48 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
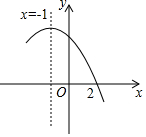 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
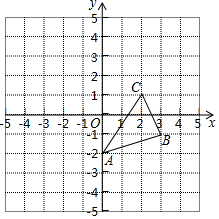 如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,-2),B(3,-1),C(2,1).
如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,-2),B(3,-1),C(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com