
����Ŀ����1����֪����ͼ1��![]() Ϊ�ȱ������Σ���
Ϊ�ȱ������Σ���![]() Ϊ
Ϊ![]() ���ϵ�һ���㣨��
���ϵ�һ���㣨��![]() ����
����![]() ��
��![]() �غϣ�����
�غϣ�����![]() Ϊ�����ȱ�
Ϊ�����ȱ�![]() ������
������![]() .��֤����
.��֤����![]() ����
����![]() ��
��

��2����ͼ2����![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �ϵ�һ���㣨��
�ϵ�һ���㣨��![]() ����
����![]() ��
��![]() �غϣ�����
�غϣ�����![]() Ϊ��������
��������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ����ʱ�뷽�����У�������
����ʱ�뷽�����У�������![]() ������⣨1����������룺��
������⣨1����������룺��![]() �Ķ��������߶�
�Ķ��������߶�![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ����˵�����ɣ�
֮��Ĺ�ϵ����˵�����ɣ�
��3����ͼ3���ڣ�2���������£���![]() ����
����![]() ���ӳ������˶�����
���ӳ������˶�����![]() Ϊ��������
��������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ����ʱ�뷽�����У�������
����ʱ�뷽�����У�������![]() .
.
�����⣨2���Ľ��ۻ���������ֱ��д����������֤��
������![]() ����
����![]() ��
��![]() ��ֱ��д��
��ֱ��д��![]() �ij�.
�ij�.
���𰸡���1�������������ڡ�DCE��120������2����DCE��90��, BD2+CD2��DE2��֤������������3������2���еĽ��ۻ���������AE��![]() .
.
��������
��1���ٸ��ݵȱ������ε����ʾͿ��Եó���BAC=��DAE=60����AB=BC=AC��AD=DE=AE�������Ϳ��Եó���ABD�ա�ACE�����ɵó����ۣ�������ABD�ա�ACE���Լ��ȱ������ε����ʣ��Ϳ��Եó���DCE��120����
��2�����ж���ABD�ա�ACE��SAS�����ó���B=��ACE=45����BD=CE����Rt��DCE�У����ݹ��ɶ����ó�CE2+CD2=DE2�����ɵõ�BD2+CD2=DE2��
��3�������ã�2���еķ����ó�BD2+CD2=DE2���ڸ���Rt��BCE�У�BE=10��BC=6�����![]() �����ó�CD=8-6=2����Rt��DCE�У����
�����ó�CD=8-6=2����Rt��DCE�У����![]() ��������ADE�ǵ���ֱ�������Σ����ɵó�AE�ij���
��������ADE�ǵ���ֱ�������Σ����ɵó�AE�ij���
��1������ͼ1���ߡ�ABC����ADE�ǵȱ������Σ�
��AB��AC��AD��AE���� ACB����B�� 60����
��BAC����DAE��60����
���BAC����DAC����DAE����DAC��
���BAD����EAC��
����ABD����ACE��
 ��
��
���ABD�ա�ACE��SAS����
��BD��CE��
�ڡߡ�ABD�ա�ACE ,
��ACE����B��60��,
���DCE����ACE +��ACB��60��+60����120����
��2����DCE��90��, BD2+CD2��DE2��
֤������ͼ2���ߡ�BAC����DAE��90����
���BAC����DAC����DAE����DAC��
����BAD����CAE��
����ABD����ACE��
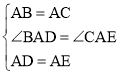 ��
��
���ABD�ա�ACE��SAS����
���B����ACE��45����BD��CE��
���B+��ACB����ACE+��ACB��90����
���BCE��90����
��Rt��DCE��CE2+CD2��DE2��
��BD2+CD2��DE2��
��3���٣�2���еĽ��ۻ�������
���ɣ���ͼ3���ߡ�BAC=��DAE=90����
���BAC+��DAC=��DAE+��DAC��
����BAD=��CAE��
����ABD����ACE��

���ABD�ա�ACE��SAS����
���ABC=��ACE=45����BD=CE��
���ABC+��ACB=��ACE+��ACB=90����
���BCE=90��=��ECD��
��Rt��DCE��CE2+CD2=DE2��
��BD2+CD2=DE2
�ڡ�Rt��BCE�У�BE=10��BC=6��
![]()
��BD=CE=8��
��CD=8-6=2��
��Rt��DCE��
![]()
�ߡ�ADE�ǵ���ֱ�������Σ�
![]()


 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ������ͼ1����������ABCD���ڲ�������DAE����ABF����BCG����CDH������������ȫ�ȵ��������á�DAE�ա�ABF�ա�BCG�ա�CDH���Ӷ����ı���EFGH�������Σ�
���̽������ͼ2��������ABC���ڲ�������1����2����3��AD��BE��CF�����ཻ��D��E��F���㣨D��E��F���㲻�غϣ���
��1����ABD����BCE����CAF�Ƿ�ȫ�ȣ�����ǣ���ѡ������һ�Խ���֤����
��2����DEF�Ƿ�Ϊ�������Σ���˵�����ɣ�
��3����ͼ3����һ��̽�����֣���ABD�����ߴ���һ���ĵ�����ϵ����BD��a��AD��b��AB��c����̽��a��b��c����ĵ�����ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
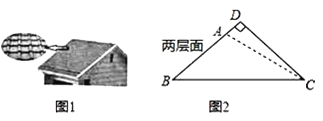
����Ŀ��̫���ܹ���������ִ���ɫ��������֮һ�����������Լ��ݶ��Ľ��ɹ�����棬�Ľ�ǰ�ݶ�������ABC��ͼ2��ʾ��BC=10�ף���ABC=��ACB=36�����Ľ���D��BA���ӳ����ϣ��ҡ�BDC=90������Ľ���������������Ӳ���AD�ij����������ȷ��0.1�ף�
���ο����ݣ�sin18���0.31��cos18���0.95��tan18���0.32��sin36���0.59��cos36���0.81��tan36���0.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ܶ������ϲ����ͷ��Ʒ���ã���Ӱ�����彡���ָ���ͥ���Ӳ���Ҫ�Ŀ�����Ϊ��ij����ѧ��ȤС��Ա���ͬѧһ��������Ʒ����������˵��飬���¿ɷ�Ϊ���֣�A����ˮ��B��ƿװ��Ȫˮ��C��̼�����ϣ�D����̼�����ϣ�����ͳ�ƽ��������������ͳ��ͼ������ͳ��ͼ�ṩ����Ϣ�������������
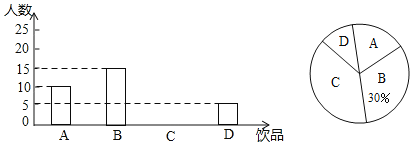
��1������༶�ж�����ͬѧ������ȫ����ͳ��ͼ��
��2�����ð�ͬѧÿ��ÿ��ֻ����һ����Ʒ��ÿ�ֽ���һƿ���۸����±�������ð�ͬѧÿ��������Ʒ���˾������Ƕ���Ԫ��
��Ʒ���� | ��ˮ | ƿװ��Ȫˮ | ̼������ | ��̼������ |
ƽ���۸�Ԫ/ƿ�� | 0 | 2 | 3 | 4 |
��3��Ϊ���������õ�����ϰ�ߣ������ξ��������ð�ˮ��5����ί�ɲ�����������λ���ΪA��B��������λ��ΪC��D��E���������ȡ2����ί�ɲ�������ϰ�ලԱ�������б�������״ͼ�ķ������ǡ�ó鵽2����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ���Ϊ
��ͼ���Ϊ![]() ������
������![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ת180���
��ת180���![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ת180���
��ת180���![]() ����
����![]() ���ڵ�
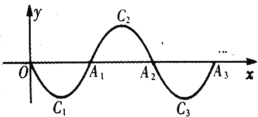
���ڵ�![]() ��������˽�����ȥ���õ�һ���������ߡ�.��
��������˽�����ȥ���õ�һ���������ߡ�.��![]() �������������ߡ��ϣ���
�������������ߡ��ϣ���![]() ____.
____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�H�ǶԽ���BD���е㣬�ӳ�DC��E��ʹ��DE=DB������BE����DF��BE��BC�ڵ�G����BE�ڵ�F������CH��FH�����н��ۣ���1��HC=HF����2��DG=2EF����3��BE��DF=2CD2����4��S��BDE=4S��DFH����5��HF��DE����ȷ�ĸ����ǣ� ��

A.5B.4C.3D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڨSOAB�У���OAB=90��.OA=AB=6.���SOAB�Ƶ�O��ʱ�뷽����ת90���õ��SOA1B1
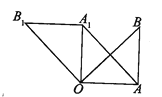
��1���߶�A1B1�ij��� ��AOA1�Ķ�����
��2������AA1����֤���ı���OAA1B1��ƽ���ı��� ;
��3�����ı���OAA1B1����� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�з���һ��ɱ�Ϊ50Ԫ��������ߣ�Ͷ���г����������ۣ������۵��۲����ڳɱ���������۲��Ź涨�����������ʲ�����90%���г����з��֣���һ��ʱ���ڣ�ÿ����������y�����������۵���x��Ԫ������һ�κ�����ϵ����ͼ��ʾ��
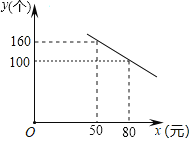
��1������ͼ��ֱ��д��y��x�ĺ�����ϵʽ��
��2���ù�˾Ҫ��ÿ����3000Ԫ�������������۵���Ӧ��Ϊ����Ԫ
��3�����۵���Ϊ����Ԫʱ��ÿ���õ����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����AC��DCΪ�ң���ACD=60�㣬PΪAB�ӳ����ϵĵ㣬��APD=30�㣮
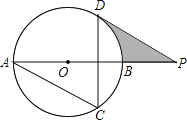
��1����֤��DP����O�����ߣ�
��2������O�İ뾶Ϊ3cm����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com