
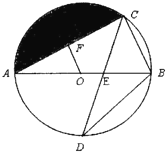
【题目】如图,AB是⊙O的直径,弦CD交AB于点E,OF⊥AC于点F,
(1)请探索OF和BC的关系并说明理由;
(2)若∠D=30°,BC=1时,求圆中阴影部分的面积.(结果保留π)
【答案】(1)OF∥BC,OF=![]() BC,理由见解析;(2)
BC,理由见解析;(2)![]() .
.
【解析】
(1)先根据垂径定理得出AF=CF,再根据AO=BO得出OF是△ABC的中位线,由三角形的中位线定理即可得出结论;
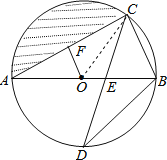
(2)连接OC,由(1)知![]() ,再根据直角三角形的性质得出AB及AC的长,根据扇形的面积公式求出扇形AOC的度数,根据阴影面积=扇形AOC的面积-△AOC的面积,即可得出结论.
,再根据直角三角形的性质得出AB及AC的长,根据扇形的面积公式求出扇形AOC的度数,根据阴影面积=扇形AOC的面积-△AOC的面积,即可得出结论.
(1)OF∥BC,OF=![]() BC.
BC.
理由:由垂径定理得AF=CF.
∵AO=BO,
∴OF是△ABC的中位线.
∴OF∥BC,OF=![]() BC.
BC.
(2)连接OC.由(1)知OF=![]() .
.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠D=30°,
∴∠A=30°.
∴AB=2BC=2.
∴AC=![]() .
.
∴S△AOC=![]() ×AC×OF=
×AC×OF=![]() .
.
∵∠AOC=120°,OA=1,
∴S扇形AOC=![]() .
.
∴S阴影=S扇形AOC﹣S△AOC=![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=![]() 时,求AD的长.
时,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=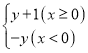 ,则称点Q为点P的“亲密点”.例如:点(1,2)的“亲密点”为点(1,3),点(﹣1,3)的“亲密点”为点(﹣1,﹣3).若点P在函数y=x2﹣2x﹣3的图象上,则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是( )
,则称点Q为点P的“亲密点”.例如:点(1,2)的“亲密点”为点(1,3),点(﹣1,3)的“亲密点”为点(﹣1,﹣3).若点P在函数y=x2﹣2x﹣3的图象上,则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是( )
A.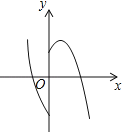 B.
B.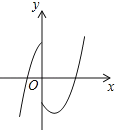
C.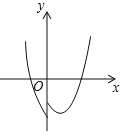 D.
D.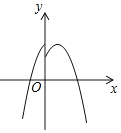
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,经过调查发现,销售单价每降低5元,每天可多售出10件,下列说法错误的是( )
A.销售单价降低15元时,每天获得利润最大
B.每天的最大利润为1250元
C.若销售单价降低10元,每天的利润为1200元
D.若每天的利润为1050元,则销售单价一定降低了5元
查看答案和解析>>
科目:初中数学 来源: 题型:
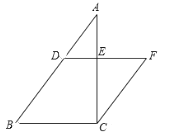
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 6,AC = 8.点D是AB边上一点,过点D作DE // BC,交边AC于E.过点C作CF // AB,交DE的延长线于点F.
(1)如果![]() ,求线段EF的长;
,求线段EF的长;
(2)求∠CFE的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
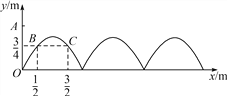
【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为![]() m,到墙边OA的距离分别为
m,到墙边OA的距离分别为![]() m,
m,![]() m.
m.
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10 m,则最多可以连续绘制几个这样的拋物线型图案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com