
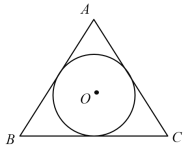
【题目】如图,已知等边![]() 的内切圆
的内切圆![]() 半径为3,则
半径为3,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
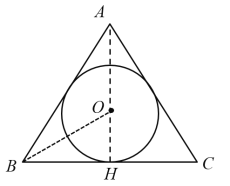
连接AO、BO,AO的延长线交BC于H,利用内心的性质得AH平分∠BAC,BO平分∠ABC,再根据等边三角形的性质得∠CAB=∠ABC=60°,AH⊥BC,则∠OBH=30°,CH=BH=![]() AB,然后利用正切的定义计算出BH即可求出AB.
AB,然后利用正切的定义计算出BH即可求出AB.
解:连接AO、BO,AO的延长线交BC于H,如图,
∵△ABC为等边三角形,等边![]() 内切圆为
内切圆为![]() ,
,
∴AH平分∠BAC,BO平分∠ABC,
∵△ABC为等边三角形,
∴∠CAB=∠ABC=60°,AH⊥BC,
∴∠OBH=30°,CH=BH=![]() AB
AB
在Rt△BOH中,∵tan∠OBC=![]() =tan30°,OH=3
=tan30°,OH=3
∴BH=![]() =3
=3![]()
∴AB=2BH=6![]()
故选:C.


科目:初中数学 来源: 题型:
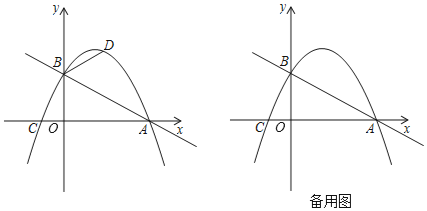
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点
与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点且与x轴的负半轴交于点
两点且与x轴的负半轴交于点![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 为直线
为直线![]() 上方抛物线上的一个动点,当
上方抛物线上的一个动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 已知
已知![]() 分别是直线
分别是直线![]() 和抛物线上的动点,当
和抛物线上的动点,当![]() 为顶点的四边形是平行四边形时,直接写出所有符合条件的
为顶点的四边形是平行四边形时,直接写出所有符合条件的![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
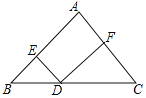
【题目】如图,在△ABC中,AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则△BED与△DFC的周长的和为( )
A. 34B. 32C. 22D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,过点
上的点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() .
.
(1)填空:点![]() _____________(填“在”或“不在”)
_____________(填“在”或“不在”)![]() 上;当
上;当![]() 时,
时,![]() 的值是_____________;
的值是_____________;
(2)如图1,在![]() 中,当
中,当![]() 时,求证:
时,求证:![]() ;
;
(3)如图2,当![]() 的顶点
的顶点![]() 是边
是边![]() 的中点时,请直接写出
的中点时,请直接写出![]() 三条线段的数量关系.
三条线段的数量关系.
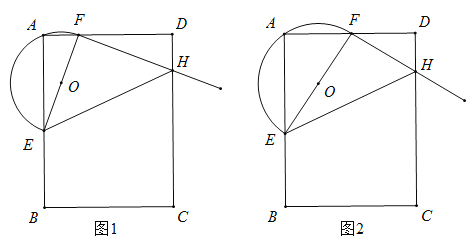
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.

(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们的东北方向距离12海里处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻艇以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻队出发到成功拦截捕鱼船所用的时间.
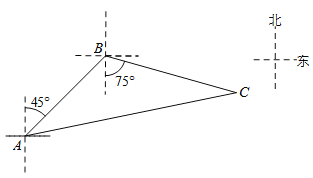
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .直线
.直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,设直线
是抛物线的顶点,设直线![]() 上方的抛物线上的动点
上方的抛物线上的动点![]() 的横坐标为
的横坐标为![]() .
.
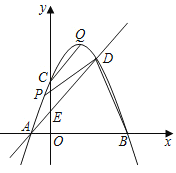
(1)连接![]() ,求证:四边形
,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)连接![]() ,
,![]() ,当
,当![]() 为何值时
为何值时![]() ?
?
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 为等腰直角三角形?若存在,请求出点
为等腰直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=![]() (k<0)的图象上.则y1、y2、y3的大小关系是( )
(k<0)的图象上.则y1、y2、y3的大小关系是( )
A.y1>y2>y3B.y3>y2>y1C.y2>y3>y1D.y1>y3>y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com