
已知二次函数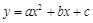 (
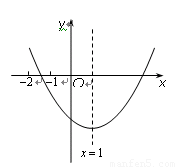
(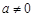 )的图象如图所示,有下列结论:①
)的图象如图所示,有下列结论:①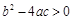 ;②
;②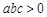 ;③
;③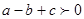 ;④
;④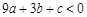 .其中,正确结论的个数是
.其中,正确结论的个数是
A、1 B、2 C、3 D、4
C
【解析】①根据图示知,二次函数与x轴有两个交点,所以△=b2-4ac>0;故本选项正确;
②根据图示知,该函数图象的开口向上,
∴a>0;
又对称轴x=-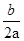 =1,
=1,
∴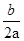 <0,
<0,
∴b<0;
又该函数图象交于y轴的负半轴,
∴c<0;
∴abc>0;故本选项正确;
③∵对称轴x=-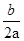
=1,
∴b=-2a,
可将抛物线的解析式化为:y=ax2-2ax+c(a≠0);
由函数的图象知:当x=-2时,y>0;即4a-(-4a)+c=8a+c>0,故本选项正确;
④根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故本选项正确;
所以这四个结论都正确.
故选D


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省金华市孝顺初中九年级(上)第一次月考数学试卷(解析版) 题型:解答题
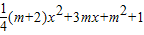 的图象经过点(0,5).
的图象经过点(0,5).查看答案和解析>>
科目:初中数学 来源:2012年江苏省盐城市中考数学试卷(解析版) 题型:解答题
 的图象经过点A(2,0)和点B(1,-
的图象经过点A(2,0)和点B(1,- ),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
 +2t.现以线段OP为直径作⊙C.
+2t.现以线段OP为直径作⊙C.查看答案和解析>>
科目:初中数学 来源:2011年广西柳州市城中区中考数学二模试卷(解析版) 题型:解答题
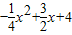 的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.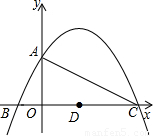
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
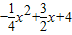 的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.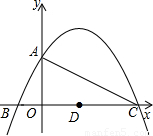
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com